Metode de gradient de rezolvare a problemelor de programare neliniare.
Întrebări: 1. Caracteristica generală a metodelor.
2. gradientul Method.
3. Metoda de coborâre mai abrupte.
4. Metoda Franca Fulfa.
5. Metoda funcțiilor de penalizare.
1. Caracteristica generală a metodelor.
Metodele de gradient sunt aproximări metode (iterative) pentru rezolvarea problemelor de programare neliniară și poate rezolva aproape orice problemă. Cu toate acestea, determinate în extremelor locale. Prin urmare, este recomandabil să se folosească aceste metode pentru rezolvarea problemelor de programare convexe, în care fiecare extremelor locale este, de asemenea la nivel mondial. Solutia de proces a problemei constă în faptul că, pornind de la un anumit punct x (inițial), o tranziție treptată este realizată într-o direcție gradF (x), în cazul în care se stabilește un punct maxim și -gradF (x) (antigradient) în cazul în care punctul de minim determinată la un punct care este soluția problemei. Astfel, acest punct poate fi în intervalul de toleranță, și la frontiera sa.
Metodele de gradient pot fi împărțite în două clase (grupuri). Primul grup cuprinde metode în care toate punctele chestionate aparțin regiunii fezabile. Aceste metode includ metoda :. Gradient, coborâre mai abruptă, Frank-Wolfe, etc. Al doilea grup include metode în care punctul investigat nu aparțin regiunii admisibile. Comun al acestor metode este metoda funcțiilor de penalizare. Toate metodele de funcții de penalizare diferă unul de altul în modul în care definiția „fin“.
Conceptele de bază utilizate în toate metodele de gradient, este conceptul funcției gradientului este direcția cea mai abruptă creștere a funcției.
La determinarea metodelor de gradient soluție proces iterativ continuă atâta timp cât:
- sau grad F (x *) = 0, (soluție exactă);
unde
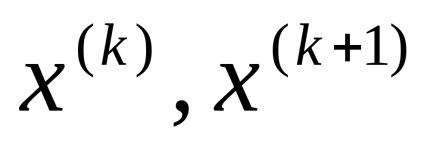
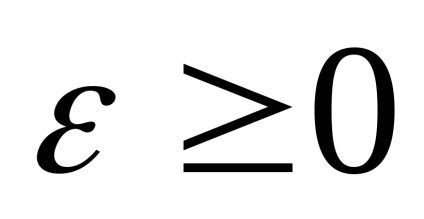
2. gradientul Method.
Imaginați-vă o persoană care stă pe pantele defileului, care trebuie să meargă în jos (în partea de jos). Cel mai natural, se pare, în direcția spre panta maximă de coborâre, și anume, direcția (-grad F (x)). S-a obținut în această strategie, numită metoda gradientului. Reprezintă o succesiune de etape, fiecare conținând două operații:
a) determinarea direcția celei mai mari Prăvăliș de coborâre (ascensiune);
b) se deplasează în direcția selectată la un anumit pas.
Alegerea corectă pas este esențială. Pasul mai puțin, cu atât mai bine rezultatul, dar mai mult de calcul. Diferite modificări ale metodei gradientului și constau în utilizarea diferitelor metode de determinare smoală. În cazul în care orice F (x), valoarea pas nu este diminuată, înseamnă că punctul „alunecat“ minim, în acest caz, trebuie să se întoarcă la punctul anterior, și de a reduce pasul, de exemplu, de două ori.
aparținând regiunii fezabile
2. Determinarea grad F (x 0) sau -gradF (x 0).
4. Determinarea punctului următor cu ajutorul formulei
x (k + 1) = x (k)
5. Determinarea F (x (k + 1)) și:
- în cazul în care se găsește o soluție;
- dacă nu, du-te la p. 2.
Notă. Dacă grad F (x (k)) = 0, atunci soluția va fi corecte.
Exemplu. F (x) = -6x1 + 2x1 2 - 2x1 x2 + 2x2 2
x1 + x2

3. Metoda de coborâre mai abrupte.
Spre deosebire de metoda gradientului, în care gradientul este determinat la fiecare pas în metoda gradientului coborâre mai abrupte găsi punctul de pornire și direcția de mișcare rezultatele în pași identice pentru a continua până când valoarea funcției scade (crește). Dacă, în orice etapă F (x) a crescut (scăzut), mișcarea în această direcție este oprită, ultimul pas este eliminat complet sau parțial, și calculează o nouă valoare a gradientului și o nouă direcție.
aparținând regiunii fezabile,
2. Determinarea grad F (x 0) sau -gradF (x 0).
4. Determinarea punctului următor cu ajutorul formulei
x (k + 1) = x (k)
5. Determinarea F (x (k + 1)) și:
- în cazul în care se găsește o soluție;
a) atunci când caută min: - în cazul în care F (x (k + 1)) - dacă F (x (k + 1))> F (x (k)) - trecerea la pasul 2 ;. b) atunci când caută max: - esliF (x (k + 1))> F (x (k)) - salt la pasul 4 ;. - Dacă F (x (k + 1)) Note: 1. Dacă în grad F (x (k)) = 0, atunci soluția va fi corecte. 2. Avantajul metodei celei mai abrupte coborâre este simplitatea și reducerea plăților, ca grad F (x) nu este calculat la toate punctele care importante pentru probleme la scară largă. 3. Un dezavantaj este faptul că măsurile trebuie să fie mici, astfel încât să nu dor de punctul de optim. Exemplu. F (x) = 3x1 - 0,2x1 2 + x2 - 0,2x2 2 x1 + 2x2

4. Metoda Frank-Wolfe.
Metoda este utilizată pentru a optimiza funcția neliniară obiectiv cu constrângeri liniare. În vecinătatea punctului unei funcții obiectiv neliniar este înlocuită cu o funcție liniară, iar problema se reduce la soluția succesivă a problemelor de programare liniară.
1. Definiție 0 x = (x1, x2, ..., xn), aparținând regiunii admisibile și F (x 0), k = 0.
2. Definiția grad F (x (k)).
Funcția 3. Build
4. Determinarea max (min) f (x) cu constrângeri inițiale. Să-ți fie un punct Z (k).
5. Determinarea etapa de calcul x (k + 1) = x (k) +




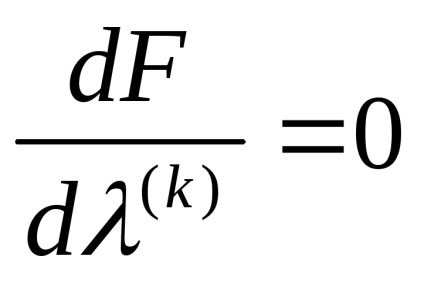

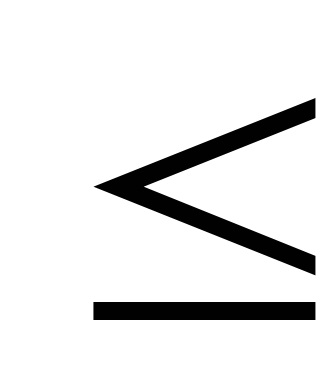
6. Determinarea F (x (k + 1)) și verificați necesitatea unor calcule suplimentare:
- sau în cazul în grad F (x (k + 1)) = 0, atunci soluția este găsită;
- dacă nu, du-te la p. 2.
Exemplu. F (x) = 4x1 + 10x2 -X1 -x2 2 2
5. Metoda funcțiilor de penalizare.
Să presupunem că avem nevoie pentru a găsi F (x1, x2, ..., xn)
Gl (x1. x2, ..., xn)
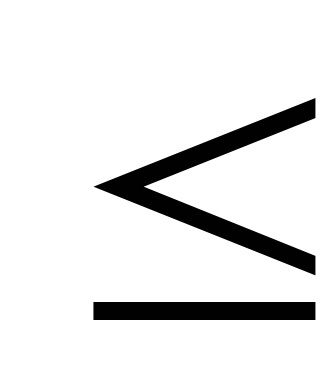
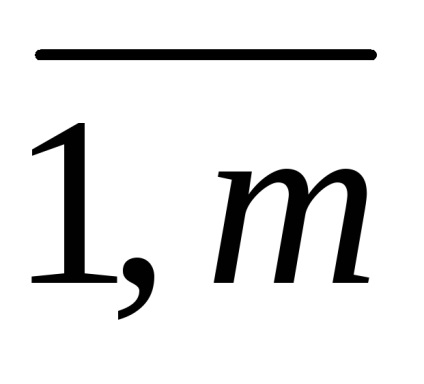
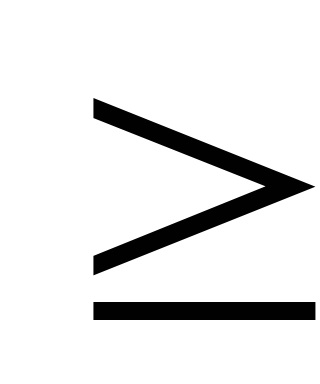
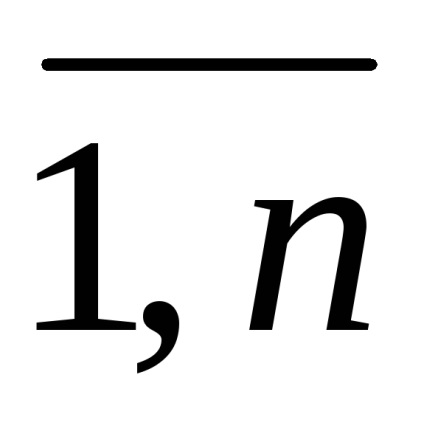
Funcțiile F și Gl - convexe sau concave.
Ideea metodei funcției penalizare este de a căuta o nouă valoare optimă a funcției obiectiv Q (x) = F (x) + H (x), care reprezintă suma funcției obiectiv original și funcția H (x), definit de constrângeri de sistem și numita funcție de penalizare. funcții de penalizare construite în așa fel încât să se asigure o revenire rapidă la intervalul admisibil, sau imposibilitatea de a ieși din ea. Metoda funcție de penalizare reduce problema unei extremum condiționate la soluția unei secvențe de sarcini la un extremum necondiționat, este mai ușor. Există mai multe modalități de a construi funcții de penalizare. Cel mai adesea este:
unde
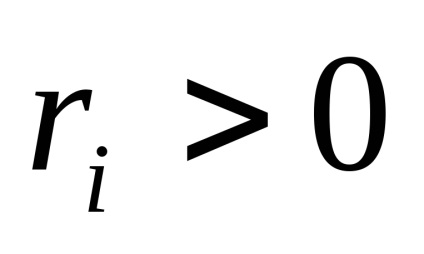
- mai puțin
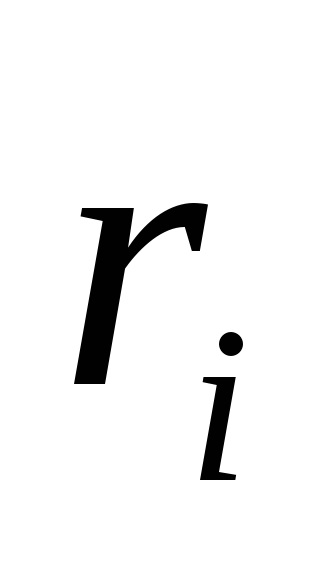
- începe cu o soluție mică
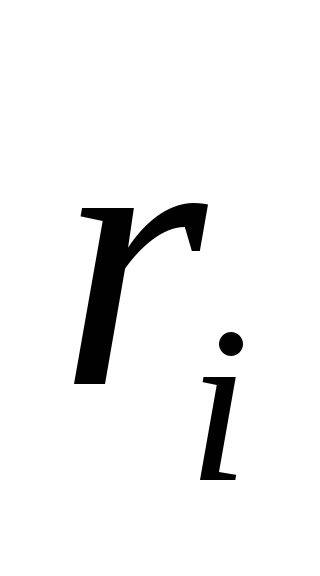
Cu ajutorul funcției de pedeapsă, se deplasează în mod constant de la un punct la altul, până când, până când vom obține o soluție acceptabilă.
1. Determinarea punctului de pornire x 0 = (x1, x2, ..., xn), F (x 0), și k = 0.
2. Selectați etapa de calcul h.
3. Se determină derivatele parțiale ale
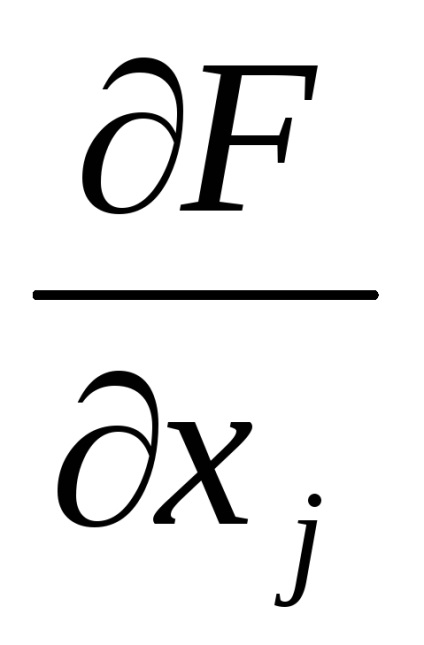
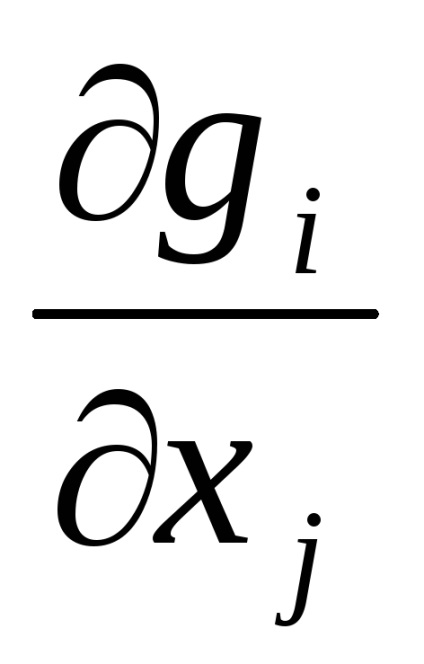
4. Să se determine coordonatele punctului următor, folosind formula:
5. Dacă x (k + 1)

a) în cazul în care - se găsește o soluție, dacă există - du-te la pasul 2 ..
b) în cazul în care soluția exactă grad F (x (k + 1)) = 0,.
Dacă x (k + 1)

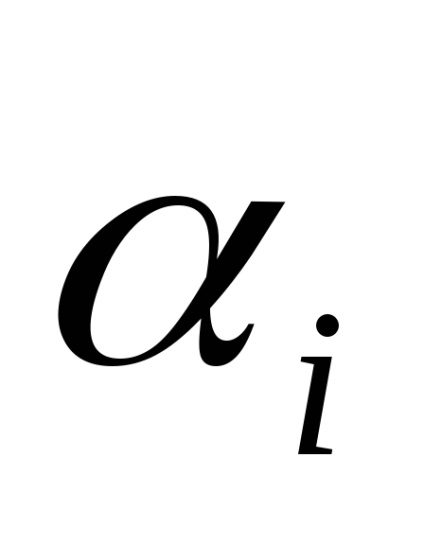
Exemplu. F (x) = - x1 2 - x2 2
(-5 X1) 2 + (x2 -5) 2