Obiectivul principal este dezvoltarea metodelor statisticii matematice pentru a obține concluzii fundamentate științific despre fenomene și procese de observații și experimente în masă. Aceste constatări și concluzii nu se referă la teste specifice de repetare care se dezvoltă acest fenomen de masă, așa cum sunt declarații cu privire la caracteristicile de probabilitate generale ale procesului, adică, probabilitățile legilor de distribuție, speranța matematică, dispersia și așa mai departe. D. O astfel de utilizare a probelor Acesta este tocmai semnul distinctiv al metodei statistice.
Să presupunem că avem informații (de obicei, destul de limitat), de exemplu, numărul de elemente defecte produse în anumite condiții de producție sau asupra rezultatelor distrugerii testării materialelor și așa mai departe. N. Datele noastre pot fi de interes direct în sensul de informații cu privire la calitatea unui anumit partid produse. Aceleași probleme statistice apar atunci când ne aflăm pe baza acelorași informații încep să tragă concluzii cu privire la o gamă mai largă de fenomene. De exemplu, am putea fi interesați de calitatea procesului, pentru care estimăm probabilitatea de a obține produsul este defect sau durata medie de viață a produsului. În acest caz, considerăm materialul recoltat nu este de dragul ei, ci doar ca un fel de un grup de testare sau a unui eșantion care reprezintă doar o serie de rezultate posibile pe care le-ar putea întâlni în continuarea procesului de masă în observațiile atmosferă. Concluzii și estimări bazate pe observații ale materialului, reflectă compoziția unui grup de test aleatoriu și, prin urmare, sunt considerate estimări brute ale naturii probabilistă. În multe cazuri, teoria indică modul cel mai bine pentru a utiliza informațiile disponibile pentru posibile performanțe mai precise și fiabile, care indică gradul de fiabilitate al concluziilor, din cauza informațiilor de stoc limitate.
A doua problemă - testarea ipotezelor - este că vom face o presupunere cu privire la distribuția de probabilitate a variabilei aleatoare (de exemplu, cu privire la valoarea unuia sau mai multor parametri ai funcției de distribuție) și să decidă dacă să fie de acord într-un sens, aceste valori ale parametrilor obținuți din observații.
Să presupunem că trebuie să examinăm trăsătura cantitative într-un partid copii ale unora dintre produsele. Verificarea parte poate fi efectuată în două moduri:
1) să efectueze o monitorizare continuă a întregului partid;
2) pentru a controla doar o parte a partidului.
Prima metodă nu este întotdeauna posibil, de exemplu, datorită numărului mare de copii în partid, din cauza costului ridicat al operațiunii de control, datorită faptului că controlul este asociat cu distrugerea unei instanțe (verificați becurile de pe durabilitatea activității sale).
În a doua metodă, o multitudine de set selectate aleatoriu de obiecte numite selective sau eșantion. Vsemnozhestvo obiecte din care eșantionul se numește populație. Numărul de obiecte dintr-un eșantion este numit mărimea eșantionului. De obicei, presupunem că mărimea populației este fără sfârșit.
Probele sunt împărțite în repetate (cu returnarea) prin eșantionare fără înlocuire (fără înlocuire).
În mod obișnuit efectuat probă noniterative, dar din cauza cantității mari (infinit) a populației efectuat calculele și concluziile sunt valabile numai pentru probe repetate.
Eșantionul trebuie să reflecte în mod adecvat caracteristicile tuturor obiectelor din populație, cu alte cuvinte, proba trebuie bytreprezentativnoy (reprezentant).
Probele diferă prin metoda de selecție.
1. eșantionarea aleatorie simplă.
Toate elementele din populația generală și sunt numerotate de la masa de numere aleatoare ia, de exemplu, orice secvență de 30 de numere consecutive. Elemente cu numărul câștigător și incluse în eșantion.
2. Selecția tipică.
Această selecție se face în cazul în care populația generală poate fi reprezentată ca o uniune de subseturi de obiecte care sunt omogene pe anumite motive, deși totalitatea această uniformitate nu este (un lot este format din mai multe grupuri efectuate la diferite întreprinderi). Apoi, pentru fiecare subgrup să efectueze o eșantionare aleatorie simplă, și proba sunt combinate toate obiectele primite.
3. Selecția mecanică.
Luate în fiecare XX (sutime) instanță.
4. Selecția de serie.
Eșantionul selectat copiile realizate la o anumită producție într-o anumită perioadă de timp.
În viitor, în populația generală ne referim nu este el însuși un set de obiecte, și setul de valori ale unei variabile aleatoare care are o valoare numerică pentru fiecare dintre obiecte. De fapt, populația ca un set de obiecte nu pot exista. De exemplu, are sens să vorbim despre o varietate de piese care pot fi produse. Folosind acest proces. Folosind unele cunoscute pentru a ne caracteristicile acestui proces, putem estima parametrii unui set inexistente de piese. Detalii Dimensiune - este o variabilă aleatoare a cărei valoare este determinată de influența mai multor factori care fac procesul. Ea are, de exemplu, poate fi interesat de probabilitatea ca această variabilă aleatoare are o valoare aparținând unui anumit interval. puteți răspunde la această întrebare, cunoscând legea distribuției acestei variabile aleatoare, precum și parametrii săi, cum ar fi M x și D x.
Deci, în afară de conceptele de populația generală ca un set de obiecte cu un anumit semn, vom lua în considerare populația generală ca x variabilă aleatoare. legislația privind distribuția și parametrii care se determină prin metoda de eșantionare.
Să considerăm un eșantion de dimensiune n. acest lucru reprezentând o populație întreagă. Prima probă x1 Valoarea va fi considerată ca realizare, ca una dintre valorile posibile ale variabilei aleatoare x1. având aceeași lege de distribuție cu aceiași parametri ca variabila aleatoare X. A doua x2 valoarea eșantionului - una dintre valorile posibile x2 variabile aleatoare cu aceeași lege de distribuție care variabila x aleatoare. Același lucru se poate spune și despre valorile x3, x4. xn.
Astfel, în proba va fi considerată ca o colecție de variabile aleatoare independente x1. x2. xn. distribuite în același mod ca x variabilă aleatoare. reprezentând populația generală .Vyborochnye valori x1, x2. xn - valori care au luat aceste variabile aleatoare, ca rezultat al 1, a 2-. n experiment -lea.
Să presupunem că populația de obiecte definite unele indicații sau o caracteristică numerică care poate fi măsurată (detalii privind mărimea, cantitatea specifică de nitrați din pepene, zgomotul motorului). Această caracteristică - variabila aleatoare X, primind la fiecare unitate specificată valoare numerică. Deoarece dimensiunea eșantionului n obținem valoarea acestei variabile aleatoare ca o serie de n numere:
Aceste numere sunt numite valori de funcții.
Printre numerele (*) poate fi același număr. În cazul în care atribuirea de valoare caracteristică, trebuie să aranjați în ordine crescătoare sau descrescătoare scriind fiecare valoare doar o singură dată, iar apoi pentru fiecare xi caracteristică valoarea scrie numărul mi. indicând cât de multe ori valoarea apare în seria (*):
veți obține o masă aproape de variațional nazyvaemayadiskretnym. Numărul mi se numește frecvența i -goznacheniya trăsătură.
Este evident că xi în seria (*) poate fi diferit de la xi la un număr de variante. Este de asemenea evident că egalitatea
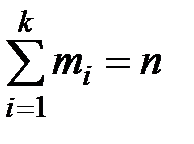
În cazul în care intervalul dintre cele mai mici și cele mai mari valori ale caracteristicii în secțiunea de probă în mai multe intervale egale de lungime, fiecare interval asociază un număr eșantion de valori de funcții, capturate în acest interval, vom obține numărul de variație interval. Dacă atributul poate lua orice valoare dintr-un anumit interval de timp, adică o variabilă aleatoare continuă, proba trebuie să fie atât de precis următor. Dacă numărul de interval variații per interval [AI; ai + 1) se înlocuiește cu minciună în numărul din mijloc (ai + ai + 1) / 2, obținem gama variațional discret. Această înlocuire este destul de natural, deoarece, de exemplu, atunci când se măsoară dimensiunea elementelor la termen de un milimetru toate dimensiunile în intervalul [49,5; 50.5), se va potrivi cu un singur număr de 50.
Punctul estimează parametrii populației.
În multe cazuri, avem informații despre o lege variabilă aleatoare (normală, Bernoulli, uniformă și așa mai departe. P.), dar nu știu parametrii de distribuție, cum ar fi M x D x. Pentru determinarea acestor parametri metodei de eșantionare aplicate.
Lăsați un eșantion de dimensiune n este reprezentată ca o serie de variante. Să ne numim valoarea medie a eșantionului
valoare
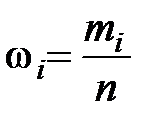
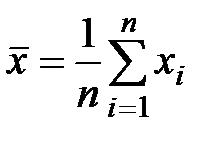
conta în mod natural valoarea M x parametru de evaluare selectivă. parametru de estimare selectivă care reprezintă estimarea numerelor nazyvaetsyatochechnoy.
Acesta poate fi considerat un punct de Dx variație estimare a populației totale.
Aici este un alt exemplu de punctul estimat. Să presupunem că fiecare obiect din totalul populației se caracterizează prin două caracteristici x și y cantitative. De exemplu, elementul poate avea două dimensiuni - lungime și lățime. Este posibil, în zone diferite pentru a măsura concentrația de poluanți în aer și se înregistrează numărul de boli pulmonare în luna populație. Puteți, la intervale regulate, pentru a compara rentabilitatea acțiunilor Corporației cu orice indice care caracterizează randamentul mediu al pieței de valori întregi. În acest caz, populația generală este o bidimensional aleatoare variabile x, h. Această variabilă aleatoare ia valori x, y din setul de obiecte din populație. Nestiind legea distribuției în comun a variabilelor aleatoare X și h, nu putem vorbi despre prezența sau adâncimea de corelare între ele, dar unele pot fi trase concluzii cu ajutorul unei metode de eșantionare.
Volumul n Exemplu în acest caz este reprezentat ca un tabel, în cazul în care
-ty obiect selectat i (i = 1,2 n.) reprezentat printr-o pereche de numere xi. yi: