Mișcarea numită curbilinie, dacă rata de m. M. și variază în mărime și direcție.
Una dintre principalele caracteristici ale acestei mișcări este considerată a fi de accelerare. miscare curbilinie este cel mai frecvent în viața reală, atunci când magnitudinea vitezei - rămâne constantă, iar direcția este în continuă schimbare. De exemplu, o mișcare uniformă de m. R. circumferențial.
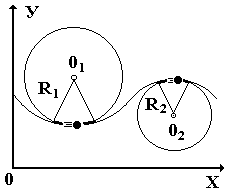
Să considerăm o mișcare m. R. De-a lungul unei curbe arbitrare.
Deoarece matematica este cunoscut faptul că o mică parte a arcului oricărei curbe netede (traiectorie) poate fi înlocuită cu un arc de cerc cu raza R1 sau R2 centrat la 01 sau 02 (Fig. 14).
Circumferința, care coincide cu limita de arc infinit de mic al unei curbe arbitrare, numit cerc de curbură.
Raza acestui cerc se numește o rază de curbură (R1 și R2), iar centrul cercului - centrul de curbură (.. T 01 și T 02 în Fig. 14). Valoarea C = 1 / R se numește o curbură a traiectoriei.
1.19. Centripetă, tangențială
și accelerație maximă
Să presupunem că într-un plan de sistem de coordonate (XOY) se deplasează m. M. Pentru a descrie o traiectorie curbă. La un moment de material punct arbitrar T1, la o viteză
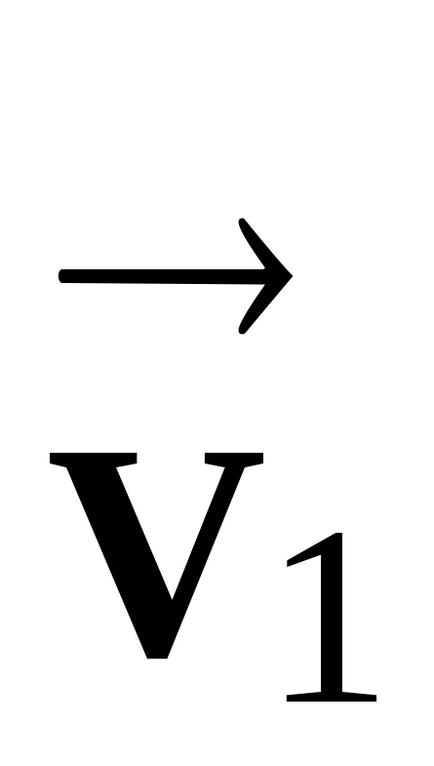

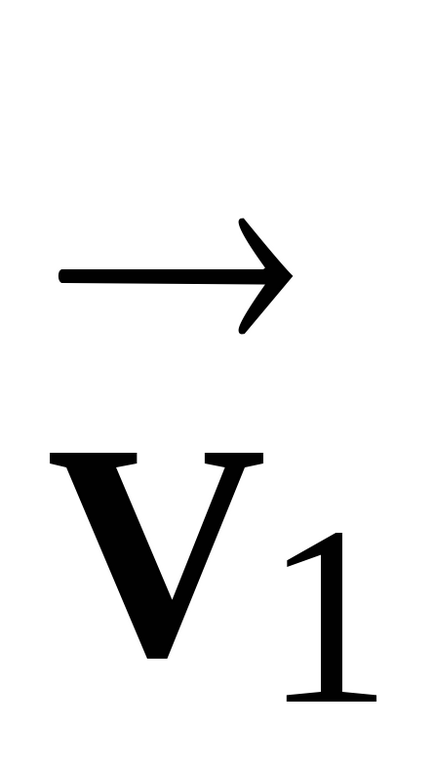
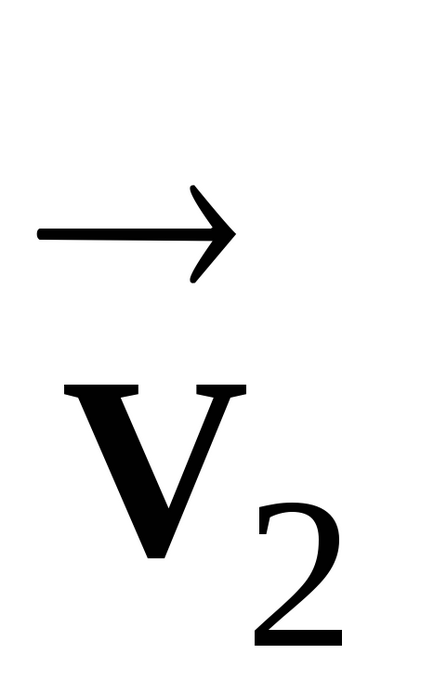
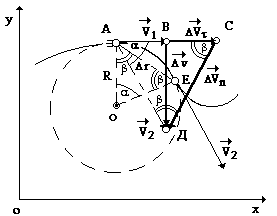
vector Fast forward
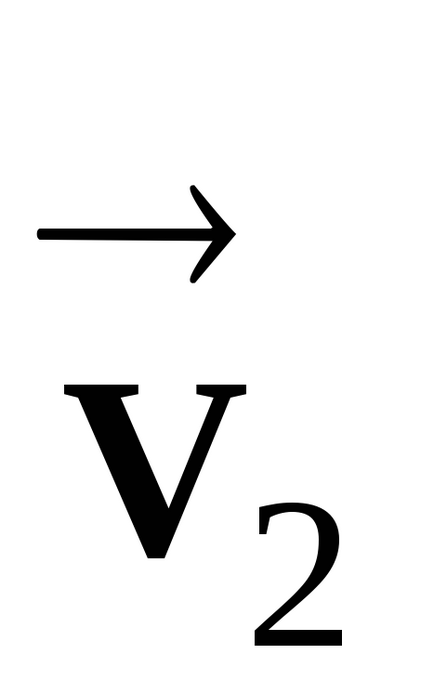
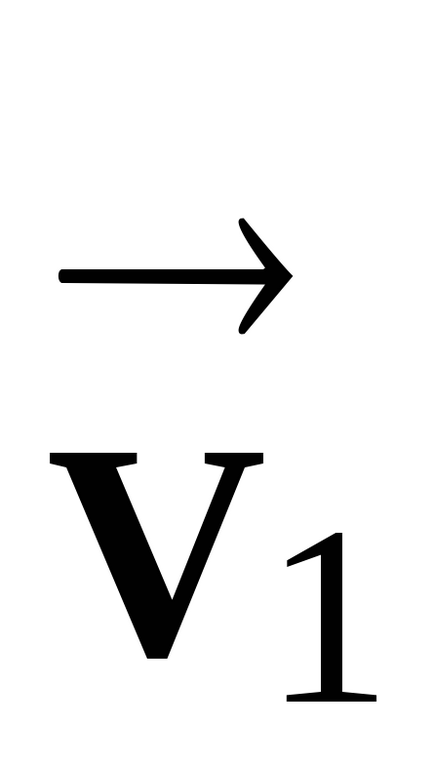
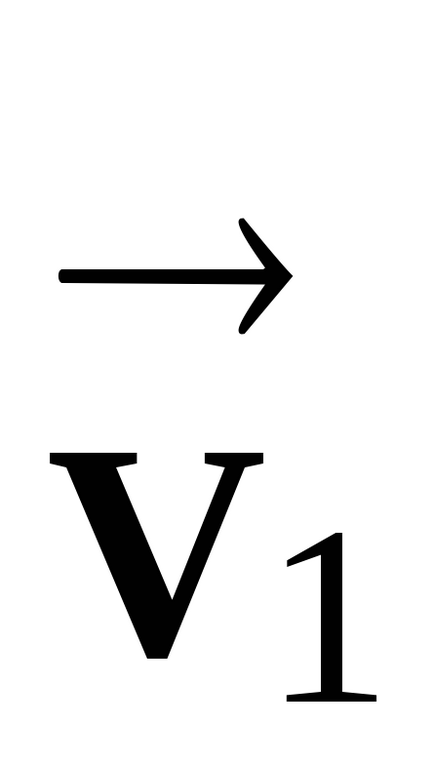
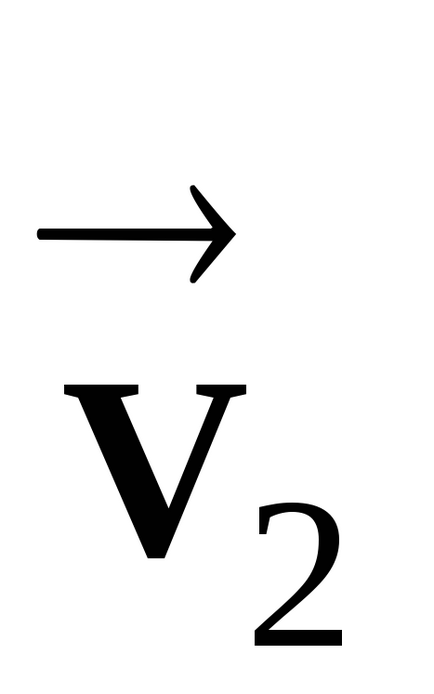
Conectați capetele vectorilor


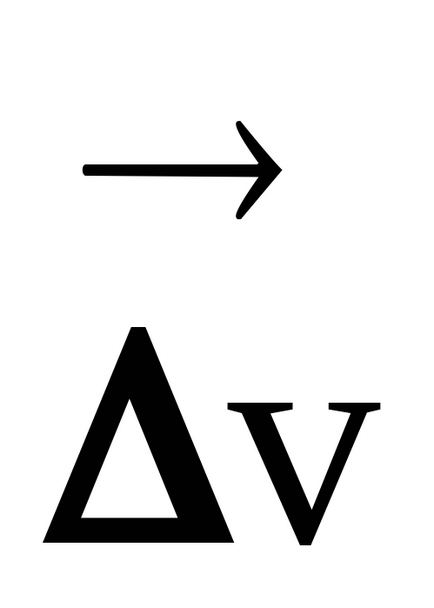
Este un vector de schimbare (creștere) a vitezei (Fig. 15) în timpul t caracterizează viteza de schimbare, atât în mărime și direcție. Pe segmentul AB (versorul
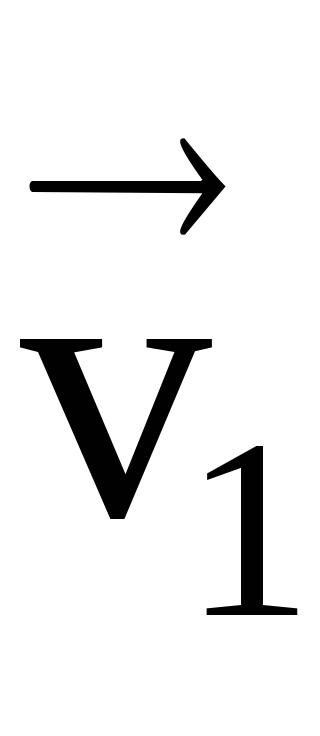

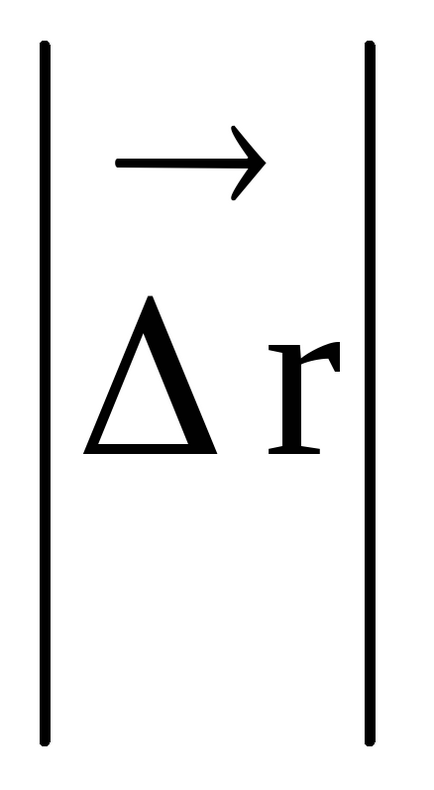
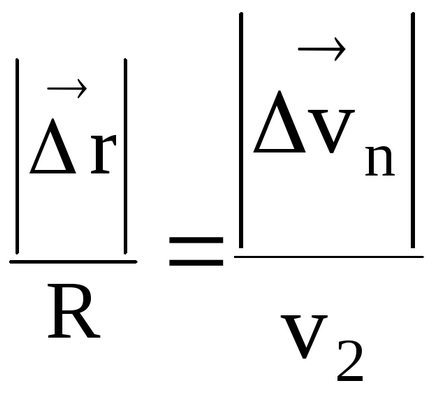
unde
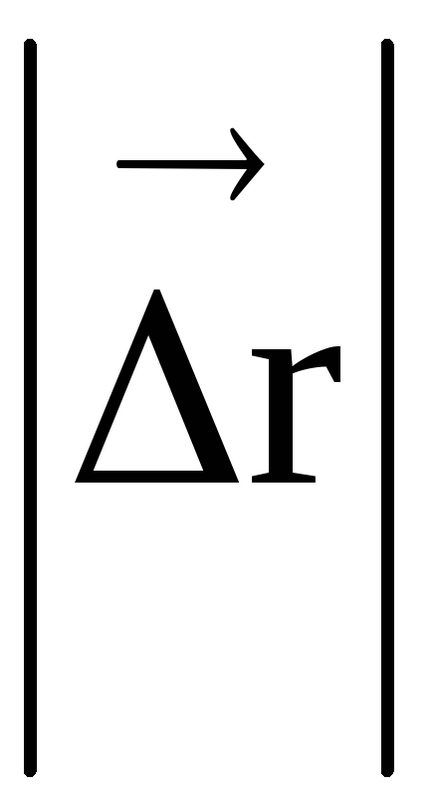
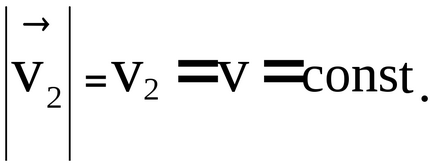
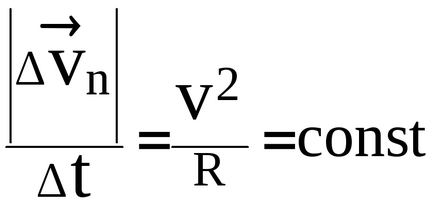
deoarece R = const și
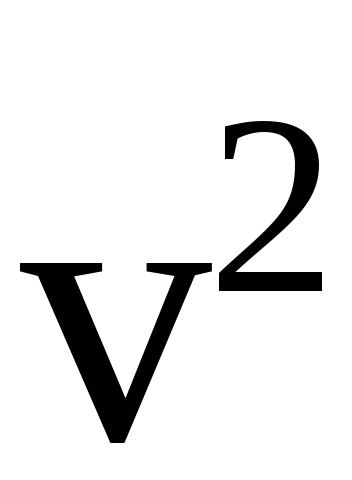
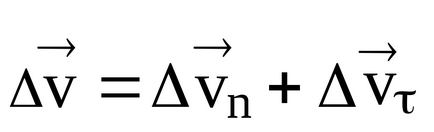
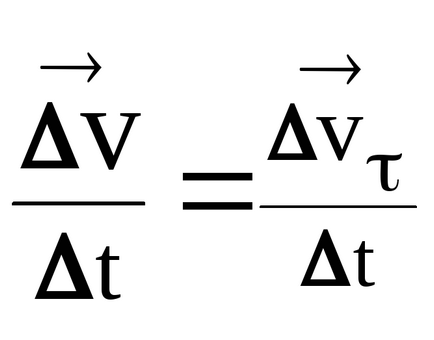
Prin definiție, accelerare instantanee, ne-am lăsat - un vector de accelerare completă
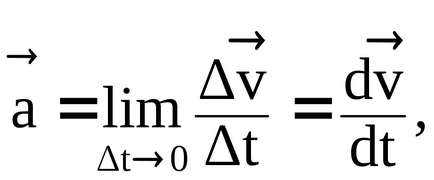
Dreapta - primul slagaemoe
al doilea mandat
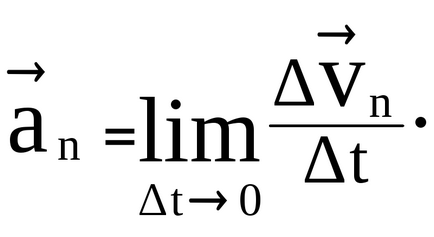
unde
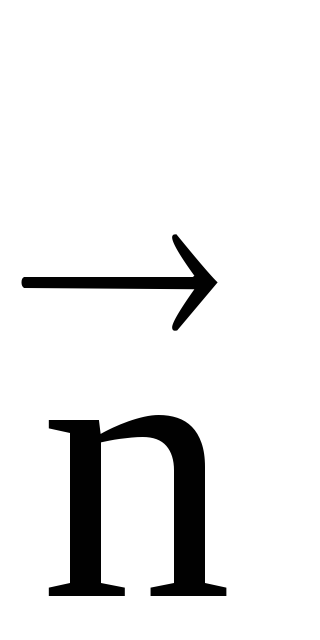
Acesta este îndreptat radial spre centrul cercului de curbură (Figura 16), deoarece trecerea la limită, când punctele A și E viteza de îmbinare
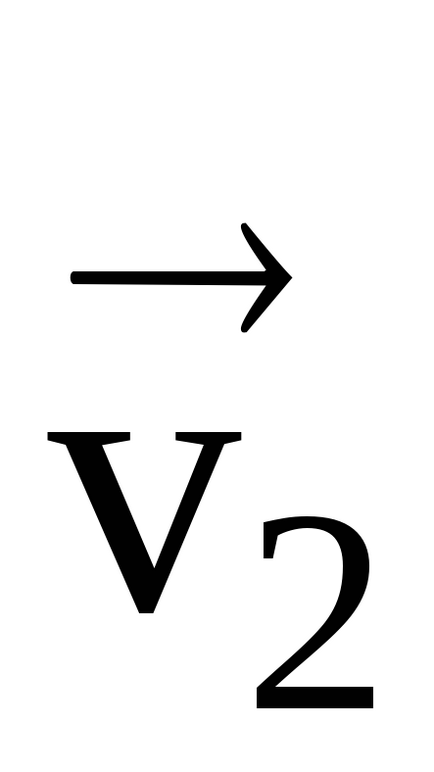
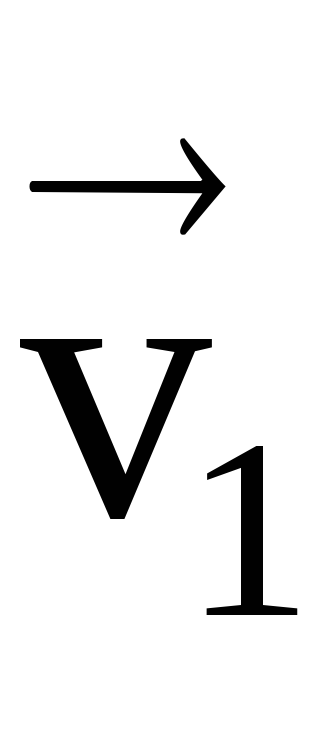
În consecință, unghiurile SDA și ADC sunt și se străduiesc să 90.
În consecință, în vectorul limită
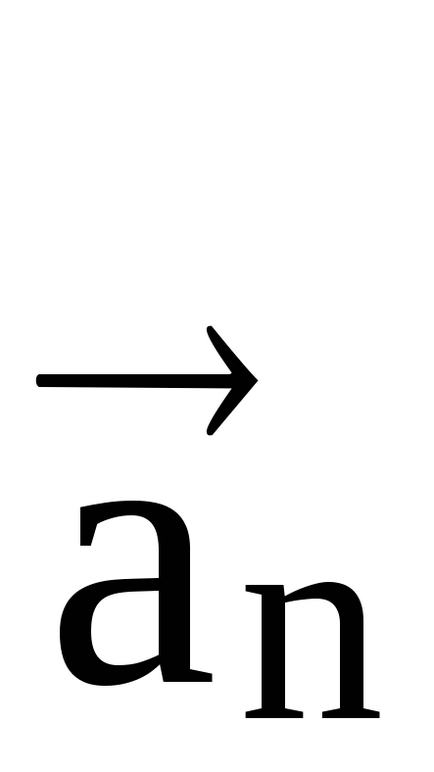
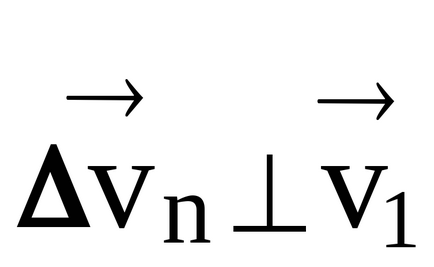
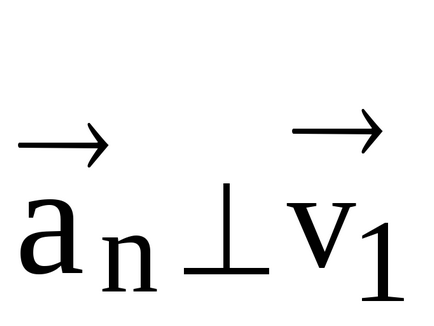
vectorul accelerație centripetă este îndreptat radial spre centrul cercului de curbură și caracterizează modificarea ratei de direcție. Luați în considerare a doua componentă a accelerației completă.
Alăturați-vă punctele C și D segmentul de linie îndreptate, care este notat cu vectorul
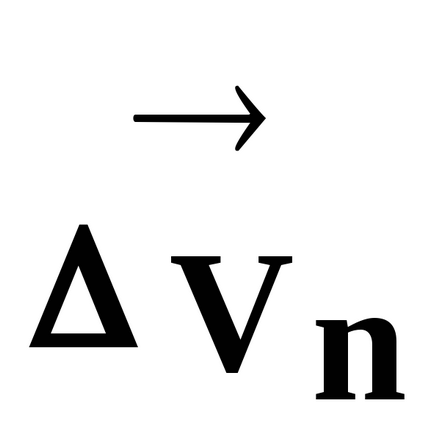
segment BC este direcționat vectorul
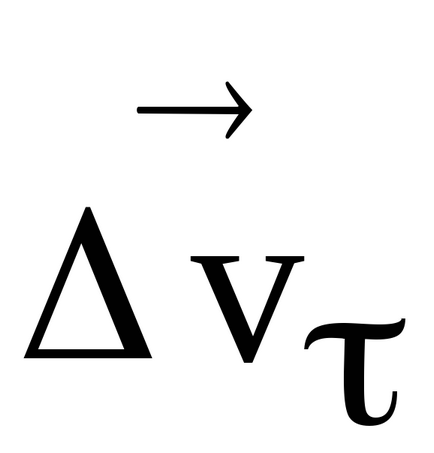

Conform Fig. 15
Din similitudinea dintre triunghiuri isoscele OUA și ASD, în cazul în care modulul
numita tangențială (tangent) accelerație, în care

(
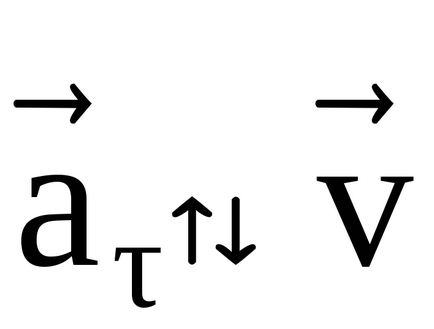
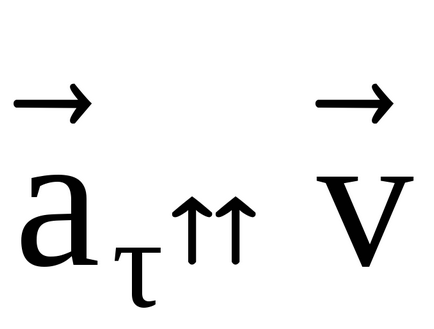
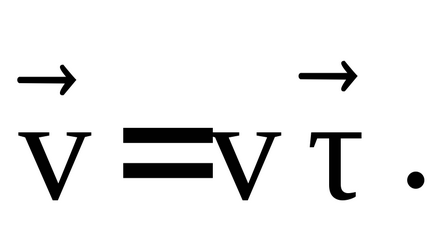
Vector tangenta caracterizează magnitudinea de schimbare a vitezei de accelerare, este direcționată de-a lungul tangenta la traiectoria în acel moment.
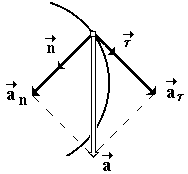
Pentru o mișcare curbilinie arbitrară a unei accelerație maximă poate fi descompusă în două componente:
vectorul accelerație maximă caracterizează schimbarea vitezei magnitudine și direcție, este îndreptată spre curbura traiectoriei.
Modul de accelerație maximă
Apariția accelerațiile normale și tangențiale observate, de exemplu, mișcarea sateliților artificiali.