Dacă totalul (5.17) dă o curbă a doua ordine nedegenerata, poate fi redus la forma canonică prin introducerea unui nou sistem de coordonate cartezian axelor de rotație evidentă printr-un anumit unghi și un transfer adecvat începe.
La transferul originii (axele paralele de traducere) coordonatele unui avion punct în sistemul de coordonate original (vechi) și coordonatele aceluiași punct din sistemul transformat (nou) legate de următoarele formule de transformare:
unde - coordonatele unui nou început în ceea ce privește sistemul original (Figura 5.16.). Formulele de transformare (5.22) sunt valabile numai în cazul în care axele ambelor sisteme sunt selectate aceeași unitate de scală.
Dacă în ecuația generală a curbei de ordinul doi (5.17) Coeficientul de munca de coordonate este zero
(), Inițială axe de coordonate sistem paralel cu axele de simetrie a curbei, și pentru conducere ecuația la forma canonică este necesară numai pentru a produce o translație paralelă axe adecvate în noul început. Acest lucru poate fi realizat în mod izolat ecuației pătrate și transferul ulterior al originii unui punct de pe formulele de transformare (5.22).
Exemplu. Reduceți ecuația formei canonice și construi dată de această curbă ecuație.
◄ În această ecuație coeficienți. . Prin urmare, se poate specifica un cerc. Selectați în ecuația de pătrate perfecte :. Înlocuirea. Ecuațiile la forma canonică. care definește o rază de cerc plan. Centrul acestui cerc este începutul unui nou sistem de coordonate. ca în sistemul original, acest centru se află la coordonatele (Fig. 5.17). Circumferinta la punctul de tangenta la axa. Noi circumferinta obține puncte de intersecție cu axa, introducerea în ecuația originală și rezolvarea ecuației pătratice rezultat. . ►
Dacă în ecuația generală a doua curbă comandă (5.17) coeficientul de non-zero, axe de coordonate nu sunt paralele cu axele de simetrie al doilea curbei ordine. Pentru a face aceste axe sunt paralele, pentru a roti coordonatei axele printr-un unghi. care este egal cu unghiul inițial între coordonate axa sistemului și o direcție pozitivă a fiecărei axe de simetrie a curbei. Acest unghi este determinat prin formula
(. Figura 5.18) Când rotirea axelor, coordonatele planului în sistem transformat (nou) și coordonatele aceluiași punct din sistemul original (vechi) legate de următoarele formule de transformare de coordonate:
Transformata inversă este:
Dacă introduceți matricea. . . transformarea (5.24) poate fi scrisă sub forma de matrice:
Transformata inversă (5.25) în formă de matrice are forma:
în care - matricea inversă.
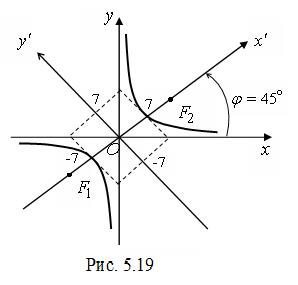
Exemplu. Construi o curbă dată de Eq.
◄ Pentru un anumit coeficienți de ecuații de ordinul doi (cm. 5.17). . restul sunt zero. Găsim Invariantele curba :. . . Din moment. . . concluzionăm că această ecuație definește o hiperbolă, axa de simetrie care nu sunt paralele cu axele de coordonate și pentru conducere ecuația la forma canonică axele de rotație necesare. Unghiul de rotație necesar se determină din formula (5.23). Din moment. numitor în formula este zero, deci. La rotirea axelor de coordonate printr-o tranziție de unghi de la vechi la noi coordonate vor fi date de (5.25) cu următoarea formulă de conversie:
Substituind în ecuația originală vechea locație la noi, avem: