Cofactor al elementului de \ (> \) \ (> \)
Numărul real: \ (k \)
Numere naturale: \ (n \), \ (i \), \ (j \), \ (s \)
Determinant unei matrice pătrate \ (\ din stânga (>> \ dreapta) \) de ordinul a \ (n \) este un polinom compus din elemente de matrice care conține \ (n! \) Conditii de forma \ (\ dreapta) ^ s >>>>> \ cdots >> \). Fiecare astfel de termen corespunde uneia din \ (n! \) Diferite seturi ordonate \ (,, \ ldots \), care au ca rezultat \ (s \) permutări de perechi de pluralitate \ (1,2, \ ldots, n \) . Valoarea determinantului este păstrată sub combinații liniare de rânduri sau coloane sau prin transpunerea matricei.
Determinantul de ordinul n-lea este scris sub forma
Determinantul matricei de ordinul doi
Determinantul ordinul al doilea constă din \ (2 \) termeni, fiecare dintre care este un produs al \ elemente (2 \):
\ (\ Det A = \ left | \\ >>>>> >>>> \ end> \ dreapta | = >>>> \)
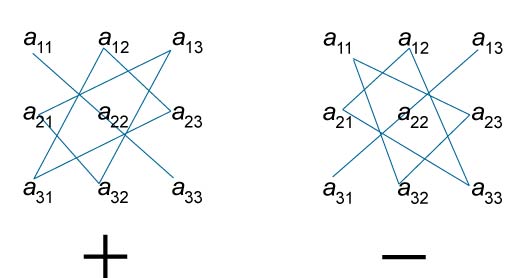
Factorul determinant al treilea ordin al matricei poate fi calculat folosind reguli Sarrusa.
Trei dintre cele șase termeni sunt incluse în cheia cu „plus“ și trei - cu semnul „minus“. Elementul triplu respectiv sunt prezentate schematic în figură.
minor
minor suplimentar \ (> \) asociat cu elementul \ (> \) pătrat matrice \ (A \) \ (n \) - lea ordin este determinant \ (\ stânga (\ dreapta) \) - th comandă corespunzătoare matricei cu \ barată (i \) - th linie și \ (j \) - th coloană.
cofactor
Cofactor \ (> \) asociat minor \ (> \), raportul
\ (> = \ Dreapta) ^ >> \)
teorema Laplace
Determinantul de ordinul n poate fi calculată folosind formula lui Laplace.
Descompunerea elementelor determinante ale rândul i-lea are forma
\ (\ Det A = \ sum \ limits_ ^ n >>>, \; \; i = 1,2, \ ldots, n \)
Descompunerea determinant prin coloana elementelor j-lea este exprimat prin formula
\ (\ Det A = \ sum \ limits_ ^ n >>> \; \ j = 1,2, \ ldots, n \)
Determinantul matricei transpuse
Valoarea determinantului nu se schimbă dacă rândurile și coloanele din matricea interschimbate (adică matricea de transpunere):
\ (\ Stânga | >>> \\ >> \ end> \ dreapta | = \ left | >>> \\ >> \ end> \ dreapta | \)
Permutare de rânduri și coloane în determinantului
Dacă două rânduri (sau două coloane) sunt interschimbate, determinantul semnului este schimbat la opusul:
\ (\ Stânga | >>> \\ >> \ end> \ dreapta | = - \ left | >>> \\ >> \ end> \ dreapta | \)
Determinantul acelorași rânduri sau coloane
În cazul în care două linii (sau două coloane) determinante sunt identice, determinantul este zero:
\ (\ Stânga | >>> \\ >> \ end> \ dreapta | = 0 \)
Multiplicarea rândul sau coloana la un determinant constant
Multiplicarea elementelor în orice rând (sau coloană) pentru același număr este echivalentă cu înmulțirea determinant pe acel număr. Cu alte cuvinte, elementele de multiplicare constante în orice rând (sau coloana) poate fi luată ca un semn al determinantului.
\ (\ Stânga | >>> \\ >> \ end> \ dreapta | = k \ left | >>> \\ >> \ end> \ dreapta | \)
O combinație liniară de elemente ale determinantului
Dacă elementele fiecărui rând (sau coloană) pentru a adăuga elementele corespunzătoare ale unui alt rând (sau coloana), înmulțită cu un factor constant, valoarea determinantului nu schimbă:
\ (\ Stânga |> + k >> \\ + k >> \ end> \ dreapta | = \ left | >>> \\ >> \ end> \ dreapta | \)