Figura 4 „Calendarul procesului de tranziție și greutatea funcției sistemului“
După cum se vede din grafic, valorile găsite pentru greutatea și caracteristicile tranzitorii sunt adevărate.
1.5. Vom calcula și amplitudine complot și faza
Caracteristicile de frecvență ale frecvenței logaritmice
Caracteristicile celulei. Verificăm vMathCad.
Secvența constatare a caracteristicilor de frecvență:
- face o schimbare în funcția de transfer p = j · ω
- a scăpa de numere imaginare la numitor
- deschide parantezele și ca rezultat în termeni similari, și de a participa la numărătorul în sumă de polinoame reale și imaginare
- scrie o expresie pentru polinoame reale și imaginare
- scrie o expresie pentru frecvența de răspuns logaritmică
- alcatuim grafice ale caracteristicilor de frecvență.
unde U (ω) - răspunsul în frecvență reală
V (ω) - caracteristica de frecvență a imaginarului
Înlocuim valorile coeficienților:
Noi construim un răspuns în frecvență:
Fig.5 „caracteristica Graph amplitudine-frecvență“
Noi construim caracteristica faze amplitudine (complot polare):
Noi construim răspunsul de fază:
Fig.7 „faza de răspuns Graph“
Am construi un răspuns de frecvență logaritmic:
Fig.8 „Programează o caracteristică amplitudine-frecvență logaritmice“
Verificați dacă caracteristicile corecte de frecvență dispozitiv de calcul utilizând MathCAD.
Scriem expresia pentru construirea de caracteristici de frecvență cu ajutorul funcțiilor încorporate în MathCAD.
A1 (w) - caracteristica amplitudine-frecvență
Fig.11 „Programează o caracteristică amplitudine-frecvență logaritmice“
Auditul a arătat că caracteristicile de frecvență ale obiectului de control construit corect.
1.6. În Matlab forma simulare de circuit și proizvedom care trece prin elementul de testare treptată. puls și un semnal sinusoidal.
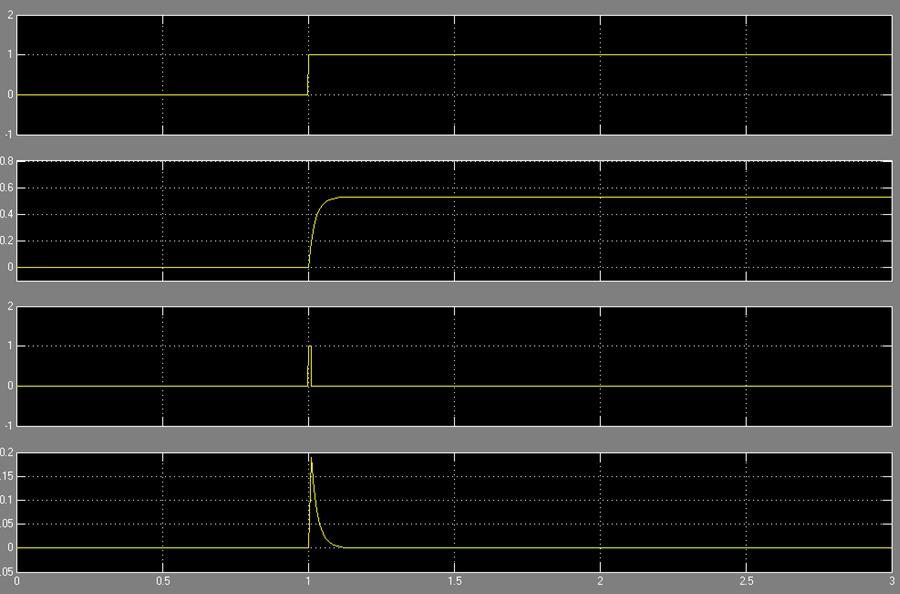
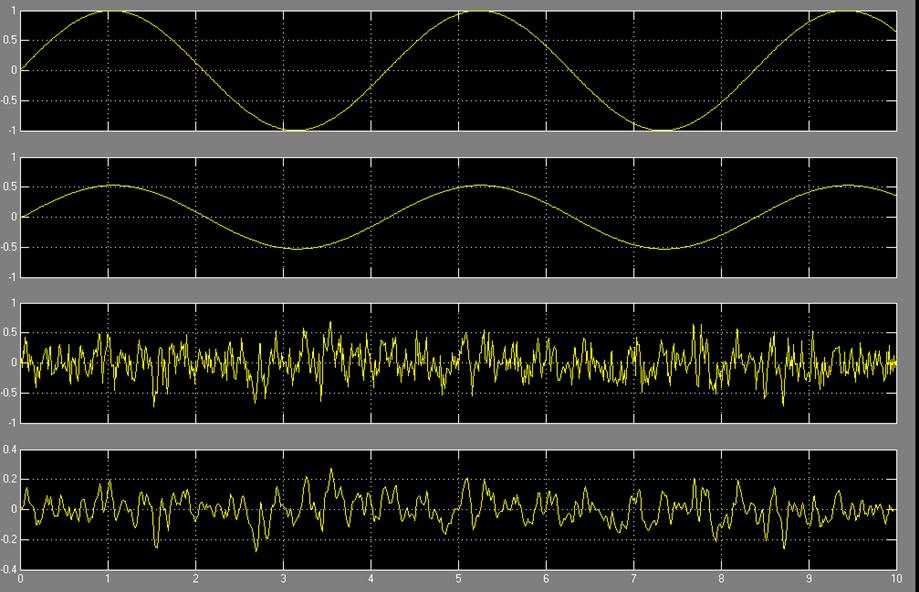
3.1. Vom găsi o funcție de transfer a canalului de acționare „de tensiune pentru armături - viteza unității“
Acționarea poate fi împărțită în două părți: piesele electrice și mecanice. partea electrică este descrisă de Kirchhoff și prin momente mecanice de inerție, și a rezistenței de sarcină.
Ecuația pentru partea mecanică a servomotorului:
în care MDV - la arborele motor
Ms - moment de rezistență
Ecuația pentru servomotor electric:
în cazul în care ea - emf în armătura
- este prezent numai când curentul în armătura
În acest caz, inerția sistemului este determinată de momentul de inerție J. În acest sens, mici fenomene tranzitorii de timp, cu toate acestea = 0.
Noi scriem sistemul de ecuații în variante: