Cartografierea a planului pe sine.
Toate conceptele care vor fi introduse de noi în această secțiune, de fapt, a fost deja studiate anterior, cu singura diferență că acum le vom introduce în termeni generali.
simetrie axială - este un tip de simetrie, în care fiecare punct al planului, de exemplu, la punctul M (Fig 1.) Printr-o anumită lege se atribuie un alt punct de același plan.
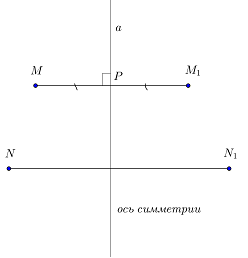
Legea, potrivit căreia această corespondență se desfășoară, după cum urmează:
Din punctul M la linia perpendiculară este obținută, iar punctul P, punctul de intersecție al perpendiculara cu axa. Întârziat segmentul RM1 = PM, și este punctul de M1. Astfel, orice punct M al planului este atribuit un punct M1 plan unic, în care:
1. MR ^ a, p - punctul de intersecție
2. RM1 = RM. din care vom obține punctul de M1
În același timp, ne-am bazat pe un fapt bine-cunoscut geometrice: din punctul M poate fi realizată doar o singură linie perpendiculară pe o anumită linie.
Operația inversă: dacă simetria axială a punctului M este atribuit un punct M1, punctul M1 corespunde unui punct M.
Exact aceleași operații pot fi efectuate și perechile de potrivire pentru N puncte N1 și același plan (fig. 1), iar dacă știm N1 punct care este atribuit unui punct N, atunci știm punctul în sine și N. Astfel, fiecare punct al planului este asociat cu un alt punct al planului. Și orice punct din planul are punctul său corespunzător.
simetrie axială este un caz special al așa-numitului plan de afișare nasebya.
Un alt caz special a planului de afișare pe sine este simetrie centrală.
M point avionul se deplasează spre un punct M1 un alt plan, în modul următor (figura 2) .:
1. o linie dreaptă MO
2. această linie continuă și pe segmentul este amânată OM1 = OM, vom obține punctul M1
M1 este atribuit un punct M.
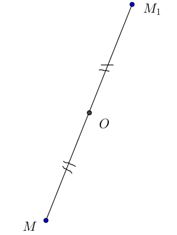
Ambele exemple prezentate hărți au următoarea proprietate:
dacă luați un segment MN lung, se va muta în segmentul M1N1 aceeași lungime, adică. e. distanța dintre oricare două puncte sunt stocate.
Se afișează planul la care toate distanțele sunt reținute nazyvaetsyadvizheniem,
t. e. „avionul se distanțează și salvat.“ Mișcările de câteva, suntem considerați două dintre ele, și anume simetria axială și simetria centrală. Acum ne arată că fiecare dintre aceste simetrii este mișcare. Este necesar să se demonstreze că orice distanțe stocate.
Pentru a dovedi această simetrie axială.
Astfel, atunci când se trece de la M M1 →, N → N1, în care PM = PM1, NQ = QN1 (Fig. 3)
Trebuie să dovedim că MN = M1N1.
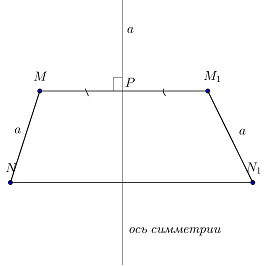
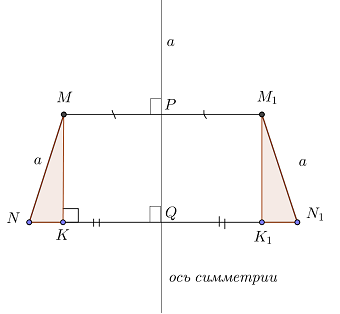
Formează desenul (Fig. 4).
Asigurați-vă suplimentar construit, construit până la punctul astfel încât MC ^ NN1,
Până atunci punctul va fi afișat la punctul K1.
Demonstram egalitatea de triunghiuri unghi drept și MNK M1N1K1. În aceste triunghiuri lungimea de interes pentru noi, este ipotenuzei, atunci trebuie să dovedească că celelalte două părți.
MK = M1K1 ca două perpendiculare pe liniile paralele.
Din Fig. 4 arată că NK = NQ - KQ și N1K1 = N1Q - K1Q. Din aceste ecuații și condiții care punctul N este afișat în punctul N1 implică faptul că NK = N1K1.
Aceasta înseamnă că două triunghiuri sunt egale în Catete, și, prin urmare, egal și ipotenuza, adică MN = M1N1, după cum este necesar.
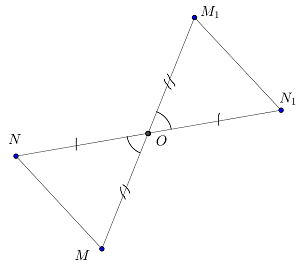
Noi acum arată că simetria centrală este, de asemenea, o mișcare. Figura supliment. 2 punctul N și N1 punct, în care este afișat primul punct în centrul de simetrie (Fig. 5).
Pentru aceasta vom construi o pe segmentul și continuarea acestuia - segmentul ON1, pentru a primi un punct N1. Astfel ON1 = ON. Noi trebuie să dovedească faptul că MN = M1N1
pe cele două părți și unghiul dintre ele (ÐMON = ÐM1ON1 ca pe verticală, iar laturile corespunzătoare ale triunghiurilor se datorează legilor centrale de simetrie).
Aceasta este, în orice simetrie centrală la distanță păstrată. Astfel, o mișcare de simetrie centrală.
Deci, ne-am uitat la planul de afișare pe sine. Considerată două exemple de planul imaginii: simetrie axială și simetrie centrală. Și am observat o circumstanță importantă, care sunt stocate toate distanțele pentru aceste transformări. Aceste transformări ale planului pe sine, care păstrează toate distanțele sunt numite mișcări. Noi am demonstrat că simetria axială este mișcarea și mișcarea este o simetrie centrală.