Pentru a efectua un studiu al funcției date privind minimul și maximul a două moduri:
- folosind primul derivat - $ f „(x) $;
- utilizând un al doilea derivat - $ f '' (x) $.
Algoritmul de cercetare folosind primul derivat cuprinde următoarele etape:
- găsirea prima derivată a unei funcții date - $ f „(x) $;
- găsirea punctelor critice ($ f „(x) = $ 0 sau nu există);
- semn de studiu $ f „(x) $ prin intermediul liniei reale;
- determinarea naturii punctului critic;
- calcularea valorii $ f (x) $ la fiecare valoare critică a variabilei.
Toate opțiunile posibile care ar putea întâmpla ca rezultat al studiului sunt cuprinse într-un singur tabel.
Explorați funcția dată pe minimă și maximă: $ y = 3x ^ $ -5x.
Găsim prima derivată a unei funcții date: $ y '= (3x ^ -5x)' = 6x- $ 5.
Punctele critice:
Deoarece derivata unei funcții date schimbă semnul de la „-“ la „+“, atunci avem un punct minim.
Se calculează valoarea unei funcții predeterminate la un nivel minim:
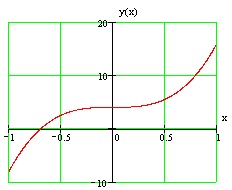
Graficul unei funcții date este prezentată în Fig.
Găsim prima derivată a unei funcții date: $ y '= (3x ^ 2)' = 9x ^ $.
Punctele critice:
- Deoarece derivata funcției dată nu se schimbă semnul când trece prin punctul critic, în acest moment nu există nici un maxim sau minim.
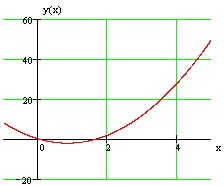
Graficul unei funcții date este prezentată în Fig.
Pentru studiul funcției dat la minim și maxim de al doilea derivat de necesitatea de a utiliza teorema următoare.
Să considerăm funcția $ y = f (x) $. Să $ $ X_ - punctul critic ($ f „(X_) = 0 $).
Apoi, această funcție are un maxim la un punct critic $ x = $ X_, dacă $ f '' (X_) 0 $.
Dacă $ f „“ (X_) = 0, la punctul critic $ $ x = $ X_, atunci această funcție $ y = f (x) $ nu poate fi determinată folosind derivata a doua natura punctului critic.
Algoritmul de cercetare folosind primul derivat cuprinde următoarele etape:
- găsirea prima derivată a unei funcții date - $ f „(x) $;
- găsirea punctelor critice ($ f „(x) = $ 0 sau nu există);
- determinarea derivata a doua a funcției dat - $ f „“ (x) $;
- semn de studiu $ f '' (x) $ la punctul critic;
- determinarea naturii punctului critic;
- calcularea valorii $ f (x) $ la fiecare valoare critică a variabilei.
Toate opțiunile posibile care ar putea întâmpla ca rezultat al studiului sunt cuprinse într-un singur tabel.
Exploreaza funcția dată la minim și maxim: $ y = 12x ^ + $, 4.
Găsim prima derivată a unei funcții date: $ y '= (12x ^ 4)' = 36x ^ $.
Punctele critice:
Găsim derivata a doua a unei funcții date: $ y '' = (36x ^) „= 72x $.
Investigați semnul $ f '' (x) $ la punctul critic: $ y '' (0) = 72 \ cdot 0 = 0 $
Deoarece al doilea derivat al unei funcții date dispare la punctul critic, nu putem determina natura unui punct critic cu ea.
Pentru a determina natura punctului critic de utilizare a primei derivate. Noi examinăm semnul $ f „(x) $ cu ajutorul liniei numărul:
- Deoarece derivata funcției dată nu se schimbă semnul când trece prin punctul critic, în acest moment nu există nici un maxim sau minim
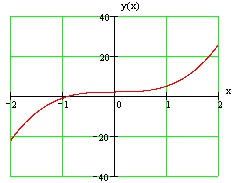
Graficul unei funcții date este prezentată în Fig.