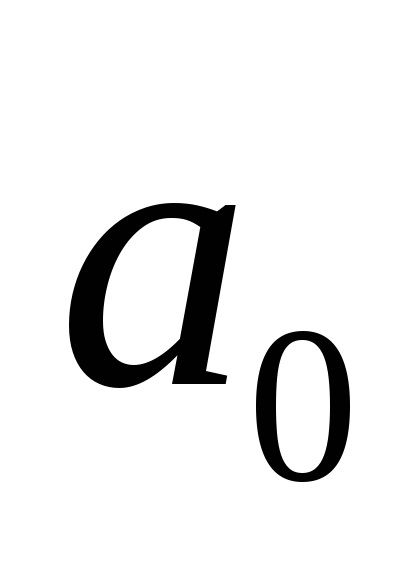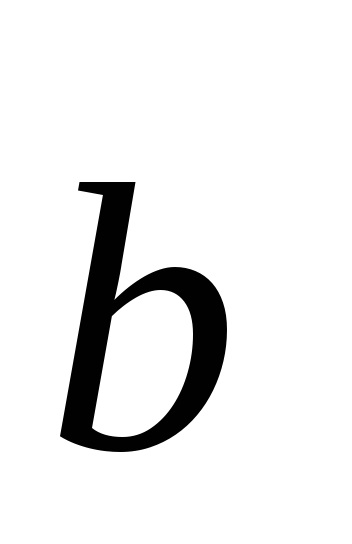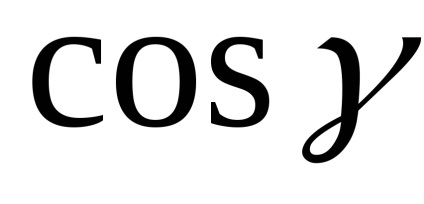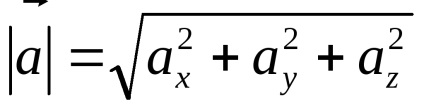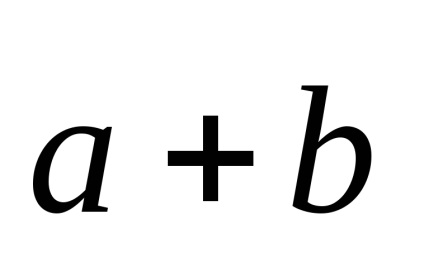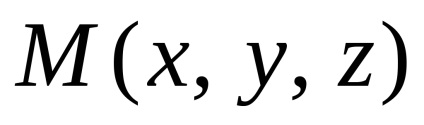vectori manipulau, scalar și produsul vectorial al vectorilor amestecați.
fundal
I. Un vector geometric.
Opredelenie.Vektorom (vector geometric) este direcționat segment de linie, adică, segment având o anumită lungime și o anumită direcție. dacă
- început vector,- capătul său, vectorul este notatsau. vector() Vector Nazyvaetsyaprotivopolozhnym .Lungimea vectorului sau modulul este numit și lungimea segmentului este notat
. Vector a cărei lungime este egală cu zero, și este notat cu vectorul nazyvaetsyanulevym . Vector a cărui lungime este egală cu unu, vector nazyvaetsyaedinichnym. Versorul a cărei direcție coincide cu direcția vectorului , nazyvaetsyaortom acest vector și se notează .
vectori
șinazyvayutsyakollinearnymi dacă se află pe aceeași linie sau linii paralele. Pentru coliniare vectori notația . Doi vectori nazyvayutsyaravnymi () Dacă au aceeași direcție și au aceeași lungime. Trei vectori în nazyvayutsyakomplanarnymi spațiu. dacă se află în același plan sau în planuri paralele.
II. Operații cu vectori.
Pe setul de vectori este introdus operațiune binar denumit plus vector. Această operație poate fi determinată fie prin regula paralelogramului (dacă vectorii
și, sunt părți la un paralelogram, atunci suma lor este un vector, unde- patru vârfuri ale paralelogramului) sau pravilomtreugolnika (în cazul în care vectorii șisunt laturile unui triunghi, atunci suma lor este vectorul).
Este ușor de verificat următoarele proprietăți ale operațiunii binare pe mulțimea de vectori:
Prin urmare, în ceea ce privește adăugarea set de vectori formează un grup abelian.
produs al vectorului
numărul deEste un vector, care are o lungimeși direcția vectorului, dacă; direcția opusă vectorului, dacă. reţineţi că.
Produsul a numărului de vector are următoarele proprietăți:
Setul de vectori geometrici
datele introduse pe spațiul operațiunilor l nazyvaetsyavektornym.
III. coordonatele vectoriale.
Luați în considerare spațiul
cu impus un sistem de coordonate cartezian. lăsași- trei vectori de unități care provin de la originea în direcțiile carteziene axele respectivși. Acești vectori nazyvayutsyaortami axe de coordonate. Lăsați vectorul De asemenea, un punct de plecare(Originea). Noi proiect sfârșitul vectoruluipe axele de coordonate. Proiecțiile rezultate pot fi scrise în videi, undeși- colțuri, care formează un vectorrespectiv cu axele de coordonateși. numereleșinazyvayutsyanapravlyayuschimi vector cosinusului . vectorși proiecțiile sale pe axele de coordonate satisfac ecuația
.
vectori troicii
spațiu vectorial nazyvaetsyabazisom . și ecuația scrisă mai sus - descompunerea vectorului pe baza. numerelesunt vector nazvaniekoordinat în raport cu baza. Deoarece coordonatele vectoruluiîn ceea ce privește această bază sunt proiecțiile vectorului pe axa de coordonate a lungimii vectorului și coordonatele sale sunt legate prin formula
.
Substituind în această ecuație coordonatele vectorului, exprimat în termeni de cosinusului direcție este ușor de a obține egalitate
,
care este îndeplinită de cosinusului direcția oricărui vector. Rețineți că cosinusului direcție sunt coordonatele vectorului unitar al vectorului
.
Deoarece coordonatele vectorului
defini-complet, puteți introduce o denumireși înlocuiți operațiuni pe vectori introduse operațiuni pe coordonatele lor. Deoarece adăugarea vectorpoate fi înlocuit cu adăugarea coordonatele lor:, adică,
și multiplicarea vectorului numărului
- multiplicarea coordonatelor de pe acest număr: sau.
egalitatea vectorilor
pentru a coordona limba presupune egalitatea de originea lor, și sunt coliniari- proporționalitatea originii lor.
Să presupunem că există două puncte
și. Apoi, vectorulpoate fi scris ca. În particular dlyaradius punct vector, avem formula sau.
articole similare