31. Figura prezintă graficul unei y funcției = f (x) și tangenta la acesta la punctul cu x0 abscisă. Găsiți valoarea derivata funcției f (x) la x0.
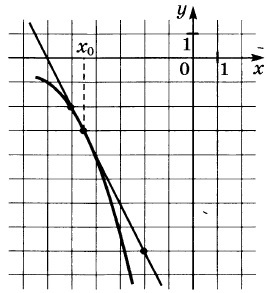
Soluție: Valoarea derivatului de la punctul de contact este egal cu panta tangentei, care la rândul său este egal cu panta tangentei la axa x. Construirea unui triunghi dreptunghic cu vârfuri la punctele A (-5; -2), B (-2, -8), C (-2; -2). Unghiul de înclinare a tangentei la axa x este egal cu unghiul adiacent la BAC unghi.
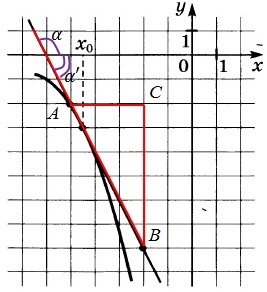
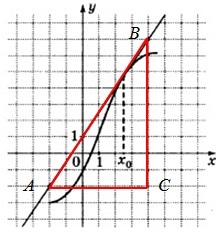
32. Figura prezintă graficul unei y funcției = f (x) și tangenta la acesta la punctul cu x0 abscisă. Găsiți valoarea derivata funcției f (x) la x0.
Soluție: Valoarea derivatului de la punctul de contact este egal cu panta tangentei, care la rândul său este egal cu panta tangentei la axa x. Construirea unui triunghi dreptunghic cu vârfuri la punctele A (-3 -3), B (5; -5), C (5, 3). Unghiul de înclinare a tangentei la axa x este egal cu unghiul adiacent la BAC unghi.
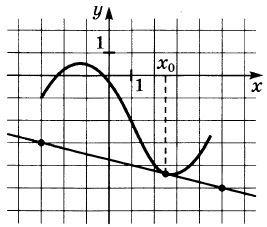
33. Figura prezintă graficul unei y funcției = f (x) și tangenta la acesta la punctul cu x0 abscisă. Găsiți valoarea derivata funcției f (x) la x0.
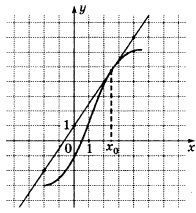
Soluție: Valoarea derivatului de la punctul de contact este egal cu panta tangentei, care la rândul său este egal cu panta tangentei la axa x. Construirea unui triunghi dreptunghic cu vârfuri la punctele A (-2, -2), B (4, 7), C (4, -2). Unghiul de înclinare a tangentei la axa x egală cu BAC unghi.
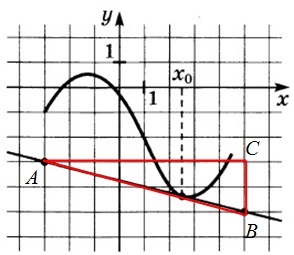
34. Cifra reprezintă un grafic al unei y funcției = f (x) și punctele marcate -5, -3, 3, 7. În unele dintre aceste puncte de cea mai mare valoare a derivatului? Ca răspuns, specificați acest punct.
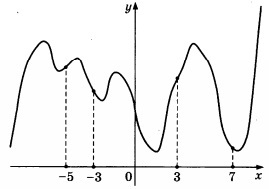
Soluție: punctele -3 și 7 funcție scade, atunci derivatul lor negativ.
La punctele 3 și -5 funcția este în creștere, atunci derivatul este pozitiv în ele.
Apoi, vom alege cea mai mare valoare a derivatului punctelor 3 și -5.
Conform sensul geometric al derivatului: derivatul în punctul de contact este egală cu panta tangentei, care la rândul său este egal cu panta tangentei la axa x.
Unghiul de înclinare (și tangente acestuia) este în mod clar mai mare la punctul 3, prin urmare, derivatul în aceasta are cea mai mare valoare.