Alinierea accente: BOLSHI`H CHI`SEL ZAKO`N
Legea numerelor mari - principiul general, în vigoare la- efectul combinat al factorilor accidentali conduce, în anumite condiții foarte generale, rezultatul este aproape nu depinde de șansă. Apropierea apariției de frecvență a unui eveniment aleator cu probabilitatea cu creșterea numărului de teste (notat cu privire la jocurile de noroc apare pentru prima dată) poate servi drept primul exemplu al acestui principiu.
La rândul său, din secolele 17 și 18. Bernoulli [1] a demonstrat teorema, care prevede că o secvență de studii independente, fiecare dintre care probabilitatea de apariție a unui anumit eveniment cerned A are aceeași valoare p, 0 <р <1, верно соотношение:
în orice # 949;> 0 și n → ∞; aici # 956; n - numărul de apariții în primele procese n, # 956; n / n - frecvența evenimentelor. Aceasta teorema lui Bernoulli a fost extins Poisson C. [2] cazul studiilor independente, unde probabilitatea evenimentului A poate depinde de numărul de încercări. Să această probabilitate pentru testul k este PK. k = 1, 2, 3, și să
Apoi, statele Poisson teorema că
în orice # 949;> 0 și n → ∞. Prima dovadă riguroasă a acestei teoreme a fost dat P. L. Chebyshevym (1846), metoda la- complet diferită de metoda Poisson și se bazează pe extrema anumitor considerente; S. Poisson terminală (2) din formula aproximativă pentru probabilitate declarat bazată pe utilizarea legii Gauss, și la acel moment nu este strict valid. În C. Poisson întâlnit mai întâi termenul „legea numerelor mari“ la ochi, el a numit generalizarea lui de teorema lui Bernoulli.
generalizarea în continuare naturală a teoremei lui Bernoulli și Poisson apare dacă observăm că variabilele aleatoare # 956; n poate fi reprezentat ca suma
variabile aleatoare independente, în cazul în care Xk = 1 dacă A apare în proces-k, iar Xk = 0 - altfel. În acest caz, matematice. așteptare E (# 956; n / n) (. coincide cu media aritmetică așteptări matematice EXk) este pentru cazul Bernoulli p și p # 175; în cazul Poisson. Cu alte cuvinte, în ambele cazuri tratate deviația aritmetică valoarea mediei aritmetice a mediilor matematice lor aritmetică. așteptări.
In lucrarea P. L. Chebysheva „cu privire la valori medii“ (1867), sa constatat că, pentru variabile aleatoare independente X1. Xn. raport
(Pentru orice # 949;> 0 și n → ∞) este adevărat conform unor ipoteze foarte generale. P. L. Cebîșev presupus matematic. așteptările EX 2 k toate delimitate de aceeași constantă, deși este o dovadă clară că limitările cerința suficiență dispersii XK. DXk = Ex.2 k - (EXk) 2. sau cerințe
Astfel, P. L. Cebîșev a demonstrat posibilitatea unei largi generalizare a teoremei lui Bernoulli. A. A. Markov a remarcat posibilitatea de generalizări suplimentare și a sugerat să folosească numele de B. h. H. generalizări la totalitatea teoremei lui Bernoulli, [și în special (3)]. Metoda Cebîșev se bazează pe un cadru precis proprietăți matematice generale. așteptările și utilizarea așa-numitele. inegalitatea lui Cebîșev [probabilitate (3) oferă o estimare a formei
această limită poate fi înlocuită cu o inegalitate mai exactă, desigur, la o limitări semnificative cm. Bernstein]. dovezi ulterioare a diferitelor forme de B. h. H. în grade diferite, sunt o extensie a metodei Cebîșev. . Aplicarea corectă "tăiat", a variabilelor aleatoare Xk (înlocuirea unor cantități auxiliare X'n, k este: H'n, k = Xk dacă | Xk - EXk | ≤ Ln și X'n, k = 0 dacă | Xk .. - EXk |> Ln în cazul în care Ln - nek- permanentă), A. A. Markov extins orele de B .... la cazurile în care nu există termenii dispersiei. Ex. a arătat că (3) deține dacă în anumite constante # 948;> 0 și L> 0 și tot n
În mod similar, putem demonstra teorema lui Khinchin (1929): în cazul în care Xn au aceleași legi de distribuție și EXn există, B h s .. (3) este îndeplinită.
Pentru sume de variabile aleatoare independente pot fi formulate într-o finală versiune B. h mai mult sau mai puțin. S. Pentru a face acest lucru, este recomandabil să meargă la un punct de vedere mai general, asociată cu conceptul de limita constanței a secvențelor de variabile aleatoare. Aleatorie valoare de secvență Y1. Yn. numit. foarte persistente, în cazul în care există o secvență de constante C1. Cn. că, în orice # 949;> 0 și n → ∞
(.. Ie Yn - Cn converge la "probabilitate" zero, în cazul în care (4) este satisfăcută de ea SUCESIUNE Cn se realizează și unde Cn = mYn mY - mediana variabilei aleatoare Y ..). Mai mult, în locul secvenței X1. Xn. variabile aleatoare independente pot lua așa-numitul. Circuit Seria (a se vedea circuitul Seria.):
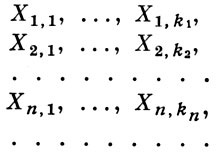
variabile aleatoare (primul indice - numărul lotului, al doilea - valoarea numărului din serie). Variabile aleatoare fiecare serie se presupune a fi reciproc independente. secvență Schema este ușor redusă la o schemă de serie, setarea k1 = 1, k2 = 2. Xn, k = Xk / n.
Apoi, forma generală a aplicabilității B. h. H. pentru sume de variabile aleatoare independente este următoarea: în condițiile în care suma maximă Yn constantă?
Răspunsul la această întrebare a fost dat de A. N. Kolmogorov (1928). Să presupunem, fără a pierde din generalitate că valorile mediane ale Xn, k este egal cu zero. Fie X # 771; n, k = Xn, k cu | Xn, K | ≤ 1 și X # 771; n, k = 0 pentru | Xn, k |> 1 - Apoi, îndeplinirea simultană a două condiții:
Este necesar și suficient pentru limitare cantități constante Yn. După cum Cn poate lua suficiența acestor condiții poate fi ușor dovedit prin Cebîșev. Dacă matematic. așteptările EXn, k exista, este ușor să se specifice condiții suplimentare sub care se poate alege Cn = EYn. ceea ce conduce la condiții necesare și suficiente pentru B. h. s. în clasic. formulare (3). Pentru o secvență de variabile aleatoare identic distribuite independent n> aceste condiții sunt reduse în conformitate cu numita Khinchine teorema, o existență matematică. așteptări. În același timp, pentru a limita constanța aritmetică Yn, în acest caz, o condiție necesară și suficientă
Este ușor de a da exemple atunci când condiția (5) nu este îndeplinită. Deci, în cazul în care acesta nu toate distribuție Xn Cauchy au o densitate de 1 / π (1 + x 2) (un roi îndeplinește funcția caracteristică e - |. T |). Aici, media aritmetică - sunt caracteristice. Funcția e - n [t / n] = e - | t |. și, prin urmare, pentru orice n au aceeași distribuție ca și termenii individuali.
Printre cele mai importante exemple de unde B. h. H. nu are loc, trebuie remarcat exemple legate de revenire din când în când în plimbări aleatorii. Ex. într-un timp simetric aleator de mers pe jos Bernoulli la revenirea Tn n-lea la punctul de plecare este suma de n variabile independente aleatoare X1. Xn. in care X1 - timp până la prima întoarcere, X2 - .. timpul între 1 și se întoarce a 2 etc. 2TN distribuție magnitudine / π n 2 converge când n → ∞ la o lege limită nedegenerat cu densitate
și egală cu zero pentru x ≤ 0. Astfel, în acest caz, distribuția mediei aritmetice a valorilor Xi. t. e. Tn / n, este situat aproximativ pe lungimea segmentului de ordinul n (în timp ce, dacă este cazul B. h. h. Se concentrează în segmente de lungime (1)).
unde de aici rezultă că, n → ∞
Un caz mai general este acoperit de termenii S. N. Bernshteyna dacă DXj
Rezultatele anterioare pot fi generalizate în diferite direcții. În primul rând, convergența a fost văzut peste tot mai sus „probabilitate“. Luați în considerare alte tipuri de convergență: .. O unitate de probabilitate medie pătratică, etc (de fapt, multe dintre condițiile de mai sus oferă convergența în medie pătratică a unui roi presupune convergenta a probabilităților). Cazul convergenței cu probabilitate una, datorită importanței sale, este alocată o specială numită „lege puternică a numerelor mari“ (a se vedea. Un mare număr de drept puternic).
Mai mult, multe teoremei tolerate, cu modificările corespunzătoare vectorilor aleatoare cu valori în spațiile euclidiene de orice dimensionalitate, din spațiul Hilbert al anumitor spații Banach. Astfel, de ex. dacă n> - o secvență de vectori aleatoare identic distribuite independent cu valori într-un spațiu Banach separabil și dacă Xn || E || (|| x || - norma x) există,
în orice # 949;> 0 și n → ∞.
Privite în forma cea mai generală B. h. S. Acesta este în strânsă legătură cu teorema ergodică. Desigur, multe teoremă extins la caz mijloc, unde X (t) - (. Vezi de exemplu [10]), proces aleatoriu, în funcție de un parametru continuu.
În cele din urmă, în loc de sumele de variabile aleatoare pot fi luate în considerare alte funcții simetrice ale acestora. Acest lucru a fost făcut A. Ya. Hinchinym (1951-1955), în legătură cu justificarea unor concluzii statistice. Mecanica [9]. Rezultat A. Ya. Hinchina poate fi explicat în următorul exemplu particular. Să Xn, Xn 1, n - coordonatele subțiri, distribuite uniform pe suprafața sferei
Apoi, pentru o clasă largă de funcții simetrice f (Xn, Xn 1, n) deține B. h. S. în sensul că valorile lor ca n → ∞ sunt constante extrem [este aproape de observația lui Levy (P. Levy, 1925) că o funcții suficient de regulate a unui număr foarte mare de variabile sunt aproape constante in majoritatea domeniu].
În cea mai mare parte din manualul vechi oferă ample statistice. date care ilustrează B. h. s. (A se vedea. Ex. [4], [11]).
Lit. [1] Bernoulli J. Ars conjectandi, opus posthumum, Basileae, 1713 (în traducere rusă - Partea a patra compozitii Bernoulli SPB 1913 ...); [2] Poisson S.-D. Recherches sur la probabilit # 233; des jugements en mati # 232; re criminelle et en mati # 232; re civile, pr # 233; CED # 233; es des r # 232; gles g # 233; n # 233; raluri du des # probabilit calcul 233, s, P. 1837; [3] Full Cebîșev PL. cit. Op. t 2, M. - L. 1947 .; [4] Markov A. A. Calculul probabilităților, 4th ed. M. 1924 [5] Teoria Bernshteyn S. N. Probability, 4th ed. M. - L. 1946 [6] distribuții Gnedenko BV Kolmogorov A. N. limită pentru sume de variabile aleatoare independente, M. - L. 1949; [7] J. Oak. Procese stochastice, Amer. din limba engleză. M. 1956; [8] probabilităților W. Grenander asupra structurilor algebrice Lane. din limba engleză. M. 1965; [9] Funcția J. A. Simetric Xinchin pe suprafețe multidimensionale, în carte. Memorie A. A. Andronova, M. 1955, p. 541-74; [10] M. Loeve, teoria probabilităților, trans. din limba engleză. M. 1962; [11] Uspensky J. V. Introducere probabilitate matematică, N. Y. - L. 1937.
- Enciclopedia matematică. T. 1 (A - D). Ed. [Et al.]: Board I. M. Vinogradov (capitole ed) - M. "Enciclopedia sovietică", 1977, 1152 col. cu ilustrații.