În calculele de caracteristicile de rezistență, rigiditate și stabilitate a utilizat geometric grinzii secțiunii transversale: pătrat, axială și momentele de inerție polare, momentele polare și rezistența axială. În plus, atunci când stabilirea rolului jucat de susținere momentele statice și momente de inerție, centrifuge.
Recall determinarea proprietăților și a metodelor de calcul al acestor parametri (Fig. 2.1).
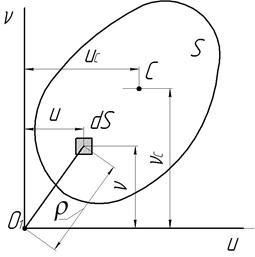
aria secțiunii transversale. În cazul în care dS - zonă de joacă elementar.
momentul static al ariei secțiunii transversale - produsul suma ariilor elementare zona de pe distanța lor față de această axă, luată peste aria secțiunii transversale. Momentul static al secțiunii transversale se măsoară în unități de lungime de gradul III (mm 3 cm 3 m 3).
momente sectionale statice în jurul axelor Ou și OV:
și în care - distanța de la centrul de greutate al secțiunii transversale, respectiv, la axele OV și Oi.
momentul static al secțiunii transversale poate fi pozitiv sau negativ. În ceea ce privește orice axă care trece prin centrul de greutate al secțiunii transversale, este zero.
momentul de inerție axial - produsul suma ariilor elementare zona de pe pătratele distanțele lor de la acea axă, luată peste aria secțiunii transversale.
Polar momentul de inerție - produsul suma ariilor elementare din zona de pe pătratele distanțele lor din punctul (pol), preluate pe toată aria secțiunii transversale.
Axială și momentele de inerție polare - valori pozitive sunt în mod semnificativ. Axială și momentele de inerție polare măsurate în unități de lungime de gradul IV (a se vedea mm 4. 4. 4 m).
momentul Centrifugal de inerție - produsul suma ariilor elementare din zona de pe coordonatele lor luate peste aria secțiunii transversale.
Un moment de inerție centrifugal este măsurat în unități de lungime de gradul IV (a se vedea mm 4. 4. 4 m) poate fi pozitivă, negativă și zero.
Prin orice punct luată în planul secțiunii, se poate realiza două axe perpendiculare între ele cu privire la care momentul centrifugal zonei este zero. Aceste axe sunt numite axele principale (denumite uneori ca axe principale de inerție). interes practic doar axă principală care trece prin centrul de greutate al secțiunii, acestea sunt numite axele centrale principale (pentru concizie, vom, în cele mai multe cazuri, pur și simplu le numesc axele principale).
Momentele axiale de inerție în jurul axelor principale (momente principale de inerție) sunt extreme - una dintre ele în ceea ce privește momentul de inerție este maximă, iar în raport cu celălalt - este minimă. Pentru calculul rezistenței și rigiditate la încovoiere, combinate cu întindere și îndoire într-un număr de cazuri, trebuie să cunoască poziția axei centrale principale și amploarea momentelor respective de inerție.
În cazul în care secțiunea transversală are cel puțin o axă de simetrie, această axă și axa perpendicular pe acestea, care trece prin centrul de greutate al secțiunilor transversale sunt principalele axe centrale.
În vederea determinării momentele principale de inerție ale secțiunilor transversale compuse din forme geometrice standard sau profile laminate simple, utilizate pe scară largă formule ale tranziției de la nivel central la axele non-centrale paralele cu acestea (fig. 2.2).
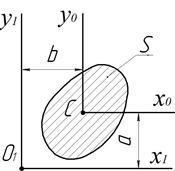
Aceste formule sunt după cum urmează: pentru momentul de inerție axial
momentul de inerție centrifug
Coordonate a și b să fie substituite cu semnele lor (a și b - coordonatele începutul unui nou sistem de coordonate cu axele vechi). În cazul particular și Ox0 Ou0 axa principală inițială, atunci avem:
Aici formula de calcul momentele de inerție al unui dreptunghi, triunghi, cerc și inele.
Un dreptunghi (Figura 2.3.). în cazul în care b # 8209; laterale paralele cu axa în jurul căreia se calculează momentul de inerție.
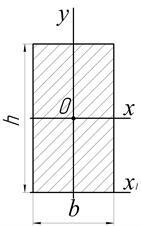
Pentru o axă care coincide cu una dintre laturile dreptunghiului (nu momentul principal de inerție).
B. Un triunghi isoscel (Fig. 2.4).
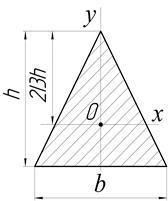
Principalele momente de inerție; .
Rețineți că formula dă o valoare a momentului de inerție al oricărui triunghi în jurul unei axe paralele cu baza sa, dar, în cazul în care triunghiul non-isoscel, axa principală a spus nu.
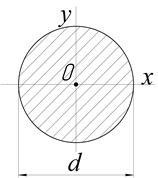
G. Ring (Figura 2.6.). în cazul în care :. raportul tub.
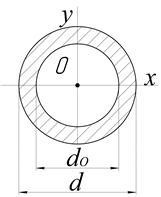
Rețineți că pentru toate roată și axa centrală inel și momentele principale de inerție în jurul acestor axe sunt egale. Același lucru este valabil pentru orice secțiune transversală, care are două momente centrale principale de inerție sunt egale.
La calcularea momentelor de inerție ale secțiunilor transversale ale complexului (compus din forme simple sau profile laminate) coordonatele centrului de greutate determinat prin formulele:
în cazul în care :; ; - respectiv zona și coordonatele centrului de greutate al fiecăreia dintre componentele cifrelor; S ;; # 8209; zonă și momentele statice ale întregii secțiuni.
Momentele de inerție (centrifugal, axial) în ceea ce privește datele de complexe secțiuni transversale ale axelor este determinată prin însumarea cifrelor respective constituie momentele de inerție aceleași axe.
În acest caz, formula utilizată pentru tranziția de la o axă centrală paralelă cu excentrică.
În aceste cazuri, atunci când secțiunea nu are nici o axă de simetrie, în primul rând calcularea momentelor de inerție unor expediente selectat axele centrale Ox0 și Ou0 (axa de referință), apoi determină unghiul de înclinare a axelor principale în raport cu valorile inițiale și momentele principale de inerție.
(. Ox0 Ou0) (. Figura 2.7) Comunicarea între momentele de inerție în raport cu axele de referință axelor și rotite cu un unghi arbitrar o are forma:
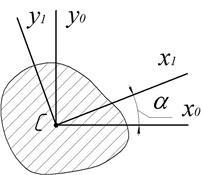
Unghiul de rotație al axelor principale în ceea ce privește sursa este determinată din relația
Această formulă dă două valori unghiulare. u = + 90 °. La>. Unghiul dă poziția axei principale, despre care momentul de inerție este maximă. Unghiul pozitiv ar trebui să fie anulată de axa x0 invers acelor de ceasornic.
Pentru a determina poziția (unghiul) a principalelor axe este posibilă aplicarea formulei:
în cazul în care :. și. - unghiurile dintre axele principale x și y, respectiv, axa x0; și - principalele momente de inerție.
momentele principale de inerție poate fi calculată prin substituirea în ea succesiv = și =. dar, în practică, este mai convenabil să utilizeze formulele care nu conțin funcții trigonometrice. Aceste ecuații au forma: