Presupunem că dat frontal și proiecțiile orizontale ale punctelor A și B (fig. 45). Dupa ce a petrecut același nume de proiecțiile acestor puncte de o linie dreaptă, obținem proiecția segmentului AB - față (A „B“) și pe orizontală ( „B“) 1).
Putem spune că acest desen (fig. 45) exprimă exact un segment de linie dreaptă? Da; dacă ne imaginăm (Fig. 46), că într-un „B“, și A „B“, a avut loc proiecția plan (adică. e., respectiv, perpendiculare la o și π2), atunci se obține intersecția acestor planuri drepte și segmentul său AB. Punctul definit de previziunile sale privind „B“ și „B“ face parte din segmentul AB.
Fig. 47 este desenul segmentului AB în sistemul π1. π2. IR3. Proiecția A 'și B „“ sunt construite în așa fel așa cum este prezentat în Fig. 18 pentru un singur punct A.
Punctele A și B sunt la distanțe diferite de fiecare dintre avioane π1. lπ2 și IR3. t. e. AB nu este paralelă cu nici una dintre ele. Astfel, nici unul dintre proiecția directă nu este paralelă cu axa de coordonate și nu perpendicular la acesta. Această linie se numește situația generală.

Fiecare dintre proeminențele mai mici decât intervalul: A'b „1); în care fiecare dintre proiecțiile liniei este la un unghi de 45 ° față de axele respective ale proeminențelor sau liniile de comunicare dintre proiecțiile.

Într-adevăr, în cazul în care (Figura 48) A "B" = A 'B' și 'B' = A '' B '', figura A "B" B'A '- un trapez isoscel și B „1 = B' 2, unde B ' "3 =" un' 3, adică unghiul a '' în '' 3 = 45 °, iar ca figura B 'B' '' o '' - .. paralelogram, fiecare dintre unghiurile "a" 1 și V'A'2 egal cu 45 °.
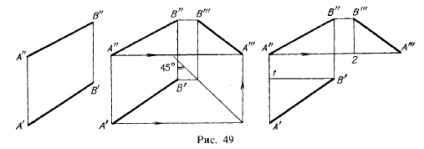
Cum de a construi pe desen topoare fără proiecții, de exemplu, proiecție profil al unui segment de linie dreaptă? Construcția prezentată în Fig. 49, în cazul în care stânga este dat sursă de desen poziția generală segmentului AB în mijloc arată utilizarea unei linii auxiliare trase la un unghi de 45 ° față de direcția de legătură B „B“, iar dreapta - construirea unei diferențe între distanțele punctelor A și B de mp π2 .. . de exemplu, de-a lungul segmentului A'l: o poziție predeterminată, chiar dacă proiecția a '' (pe link-ul a "a„), concedieze a '' A'1 = 2 și, după punctul de 2 perpendicular pe Perez
1) Ieșire cm. In § 13.