1 și valoarea maximă minimă a funcției pătratice profesor de matematică noiembrie Vetluzhskaya SOSH 2 Tatyana Anatolevna Maksimova

01 februarie (a). Se determină cea mai mare sau cea mai mică valoare a funcției ia. Găsiți-l. Cea mai mică valoare a funcției y = -1 x = -1
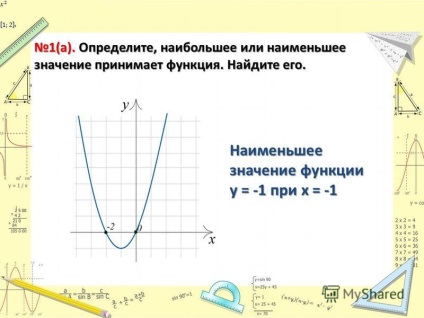
1 martie (b). Se determină cea mai mare sau cea mai mică valoare a funcției ia. Găsiți-l. Cea mai mare valoare a funcției y = 4, cu x = -1
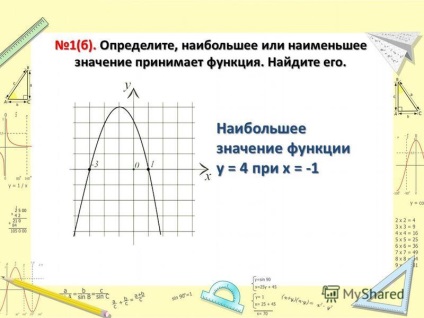
4 3. Găsiți cea mai mare și cea mai mică valoare funcției pe intervalul [-1, 2]. Cea mai mare valoare a funcției pe intervalul [-1, 2] este egal cu 0. Cea mai mică valoare funcției pe intervalul [-1, 2] este egal cu -4.
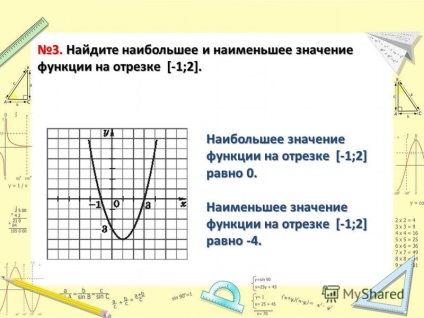
5 3. Construiește grafic, determină cea mai mare sau cea mai mică valoare a funcției ia. a) Funcția ia cea mai mica valoare de 7, atunci când x = -2. b) funcția ia cea mai mare valoare de 3/8 x = -7/16.

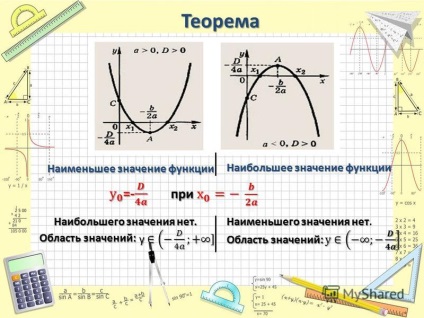
Teorema 6 Cea mai mică valoare a funcției Cea mai mare valoare a cea mai mare valoare a funcției nu este. Intervalul de valori:
7 Dido - fondatorul orașului Cartagina, prima sa regina Dido - fondatorul orașului Cartagina, prima lui regină.

8 4. Provocarea Regina Didona. 4. Provocarea Regina Didona. Potrivit legendei, forțat să fugă din orașul său natal, Dido cu tovarășii lui, a ajuns pe malul nordic al Africii și a vrut să cumpere localnici un loc pentru noua localitate. Ea a fost de acord să renunțe la o bucată de teren, dar nu mai mult decât îmbrățișează piele de vacă. Clever Dido tăiat bou ascunde pe berete înguste și extinderea acestora, a reușit să limiteze o suprafață mult mai mare decât cea care ar putea acoperi întreaga piele. Se determină cea mai mare suprafață a terenului.
10 Algoritmul pentru rezolvarea problemei. 1. Crearea unui model matematic al problemei. 2. Pune o funcție pătratică. 3. Găsiți valoarea maximă (minimă) a funcției pătratice. 4. Răspunsul la întrebarea se referă la problemei.

12 Investigarea teoremei. O consecință a teoremei. Produsul a doi factori pozitivi, a căror sumă este constantă, atinge valoarea sa maximă atunci când acești factori sunt egali. Produsul a doi factori pozitivi, a căror sumă este constantă, atinge valoarea sa maximă atunci când acești factori sunt egali.
13 Distanța dintre punctele A și B, aranjate într-o linie dreaptă, la 9 km. De la A la B merge viteza de masina de 40 km / h, la un moment dat de B în aceeași direcție ca și călăreț se deplasează cu o accelerație constantă de 32 de km / h. Se determină distanța maximă care poate fi între un autovehicul și călăreț în timpul primelor două ore de mișcare. 6. Distanța dintre punctele A și B, aranjate într-o linie dreaptă, la 9 km. De la A la B merge viteza de masina de 40 km / h, la un moment dat de B în aceeași direcție ca și călăreț se deplasează cu o accelerație constantă de 32 de km / h. Se determină distanța maximă care poate fi între un autovehicul și călăreț în timpul primelor două ore de mișcare.
14 Aparatul este de la punctul A la o distanță de decizie 40t km. Masina este de la punctul A la o distanță de 40t km, călăreț în (16t 2 +9) km distanta. Distanța dintre ele în = / 16t t / y = / 16t t / t 0 = 5/4 0 y = 16 A: 16 km
15 Tema. Dovedește teorema și corolar la acesta. 1. demonstra teorema și corolar la acesta. 2. Arătați că toate triunghiurile din perimetrul cea mai mare suprafață este echilateral. 3. Activitatea creativă. Imaginați-vă o soluție practică pentru problema conținutului pentru a gasi cele mai mari și cele mai mici valori ale unei funcții pătratice.
16 reflecție. 1. Ai primit o nouă informație, interesante, importante? 2. Cât de mult a fost clar că a studiat (1-100%)? 3. Informațiile, cunoștințele, aptitudinile vor fi utile în viitor? 4. Optați puncte au fost că te excitat, încântat, surprins, mulțumit? 5. Există interesante propriile gânduri, idei, întrebări ca urmare a studierii cursului? 6. Are dorința de a studia acest subiect a apărut, teme, probleme.