Este necesar să se găsească valoarea unui parametru, astfel încât ecuația are o soluție unică. Faceți cunoștință cu forma ecuației care definește semicercului.
Sarcină. Care este valoarea parametrului. dacă ecuația
Ea are o soluție unică?
Rescrieți un pic diferit:
Să lucrăm cu partea dreaptă:
Acum, pentru partea stângă.
Pe partea stângă avem ecuația semicercului cu centrul. Cum să înțeleagă acest lucru? cuadratura:
24 au primit cercul razei ecuației centrată în punctul. Dar, având o „taie“ rădăcina tuturor ordonatelor este mai mică decât zero, care va fi doar jumătatea superioară a cercului.
Și acest drept? Se pare că linia are doar dependența față de parametrul ecuației, deci trebuie să înțeleagă că, cu această linie se întâmplă pentru a schimba parametrul. Rețineți că, în orice punct cu abscisa 11 și ordonata 0 aparține unei linii drepte. Acesta este punctul - centrul de rotație al liniei noastre, care se poate schimba ca o pantă. și coeficientul. Suntem interesați în mod evident, în cazul atingerii directe și semicercului. Mai mult decât atât, este necesar să se găsească o pantă dreaptă, adică tangenta unghiului.
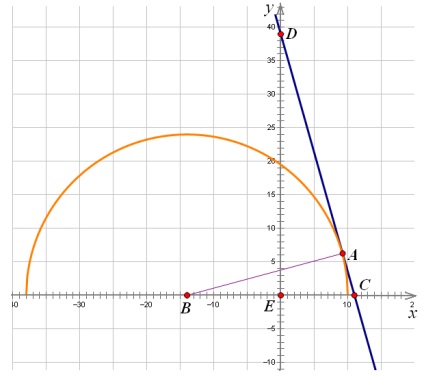
Și care se ocupă cu semicercul directe sale
Triangle - dreptunghiular, cu unghiuri drepte. piciorul. și ipotenuza. prin urmare, al doilea picior 7 este egal cu (teorema lui Pitagora).
Triunghiurile și similare (ambele dreptunghiulare și unghi egal cu unghiul drept colțuri cu laturile perpendiculare reciproc). atitudine Prin urmare, pentru aceste triunghiuri pot fi scrise laturi congruente:
O pantă linie dorită este:
Alte soluții la această problemă nu au, pentru că numai atunci când atingeți direct va avea un punct în comun cu semicercul, în toate celelalte cazuri - sau două, sau nici unul.