„Dacă doriți să învățați cum să înoate,
nu ezitați să intre în apă,
dar dacă doriți să învățați cum să rezolve problemele.
apoi le rezolva. "
D. Polya (1887-1985 g)
(Matematician. El a avut o mare contribuție
popularizarea matematicii.
El a scris mai multe cărți despre
cum să rezolve problemele și
să învețe cum să rezolve problemele.)
Algoritmul de Gauss-Jordan sisteme de ecuații liniare de rezolvare
2) Selectați elementul gazdă (orice element non-zero), în orice rând și în orice coloană, cu excepția ultimei. (Rând și coloana în care este numit lider).
3) Rulați ștergerea Iordania care duce la elementul selectat. Notă linia de conducere și toate liniile marcate anterior.
4) În cazul în care cel puțin o linie are forma (0 0 ... 0. b), b ≠ 0, atunci sistemul nu are soluții. Răspuns. sistemul este incompatibil.
5) În cazul în care toate rândurile nenule ale matricei sunt etichetate, apoi scrie în jos sistemul și pentru a găsi soluția generală. Răspuns. Soluția generală.
6) Selectați elementul principal în orice rând neetichetate și în orice coloană, cu excepția ultimei. Mergeți la pasul 3.
Pornește excepția Jordan conduce elementomaij înseamnă următoarele:
1) împart rândul lider de elementul de conducere;
2) umple spațiul liber din coloana zerourile;
3) elementele de matrice rămase numărate prin formula, numită „regula dreptunghiului.“
Imagineaza-l, în general, în mod schematic. Element de conducere va aloca cadru. Săgețile arată elementele care sunt multiplicate în numărător. Aceste elemente sunt dispuse pe diagonalele dreptunghiului format de elementul de conducere Aij. recalcula AKL elementelor și elemente care se află la intersecția dintre lider rând și coloană l. conducând coloană și rând k.
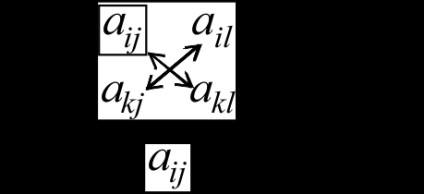
Note.
1. numărătorul este întotdeauna produsul unui element de conducere (indiferent de partea de sus a dreptunghiului este în valoare de element de antrenare) se scade produsul din elementele care sunt la intersecția rândului pivot și coloana l. conducând coloană și rând k.
2. În cazul în care linia de antrenare este elementul de zero, coloana în care se află la excluderea Jordan nu se schimba.
3. În cazul în care coloana de conducere este elementul zero, linia în care este situat la excluderea Jordan nu se schimba.
Luați în considerare exemplele de sisteme de rezolvare de către Jordan-Gauss.

Scriem matricea Augmented a sistemului

Alegerea unui element de acționare (element de antrenare va aloca frame):

Efectuați excepția Iordaniei cu elementul de conducere A13 = 1.
1) divizat linia de plumb 1;
2) umple spațiul liber din coloana a treia zerouri;
3) în principala coloană a doua linie este elementul zero (a23 = 0), astfel încât a doua linie de rescriere nemodificată (Observație 3);
4) Elementele rămase ale matricei (și anume, cele patru rânduri rămase din al treilea element) mizat pe „regula dreptunghiului.“
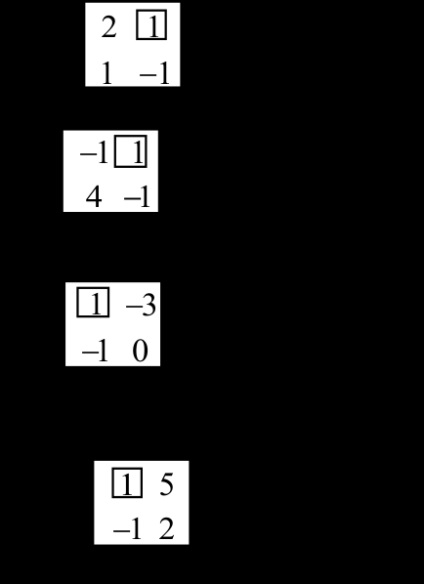
In matricea rezultată va marca primul control rând:

Acum, această matrice select plumb (orice non-zero) element orice rând neetichetate și orice coloană cu excepția ultimului, de exemplu, A21 = 1.

Efectuați excepția Iordaniei cu elementul de conducere A21 = 1:
1) divizat linia de plumb 1;
2) umple spațiul liber în prima coloană a zerourilor;
3) în a treia linie de antrenare coloană este elementul zero (a23 = 0), și, prin urmare, a treia coloană rescrie neschimbat (Nota 2);
4) se recalculează elementele rămase ale matricei „regula dreptunghi“.
Tick plumb (al doilea) rând și linia marcată anterior.
Rezultatul este o matrice:

Matricea finală a treilea rând toate elementele cu excepția elementelor din ultima coloană sunt zero. Prin urmare, sistemul este incompatibil (n. 4 în metoda algoritmului Gauss-Jordan a sistemelor de ecuații liniare de rezolvare).
RĂSPUNS: Sistemul este incompatibil.
