SCOPUL PRELEGERI: Pe baza conceptului de entropie condiționată pentru a defini informațiile reciproce, a se vedea proprietățile și de a introduce o formulă pentru a calcula valoarea medie de informare reciprocă.
Se măsoară toate măsurătorile disponibile și pentru a invalida măsurătorile sunt disponibile. Galileo Galilei
În capitolul precedent am definit entropia condiționată ca o valoare care indică o alegere medie de incertitudine în valoarea unei cantități y. Când valoarea x este cunoscută.
entropie condițional îndeplinește următoarele condiții.:
Interesul tehnologia de mesagerie este posibilitatea de a obține informații cu privire la mesajele transmise de simboluri observate la ieșirea canalului. A prezentat un operații matematice efectuate de către transmițător și receptor. Emițătorul și receptorul se numește traductoare discrete. In convertorul este secvența de intrare de simboluri de intrare ale unei benzi X, iar ieșirea este o secvență de simboluri de ieșire furnizate convertor D ansamblu poate avea o memorie internă. Simbolul de ieșire în acest caz, va depinde nu numai de pe simbolul de intrare este prezent, dar, de asemenea, pe toate cele anterioare. Obiectivul este de a cuantifica informația de simbol de ansamblul de intrare x X. conținute în simbolurile de ieșire ale ansamblului au la ieșirea canalului, inclusiv ținând cont de dependența statistică specificată.
Introducem notația informații reciproce I (x, y). În conformitate cu proprietatea entropia 5, putem scrie relația
Noi ilustrează în mod grafic entropia sistemului și informații
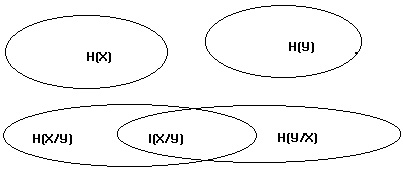
Fig. 1 Afișaj grafic de informare reciprocă.
ovaluri superioare izolate - în absența comunicării între ansambluri variabile X și Y;
Combinații ovaluri inferioare - dacă relația statistică între X și Y. ansambluri
Luați în considerare benzile X și Y, care caracterizează sistemul. Entropy ansamblu X zugrăvi oval cu o suprafață H (X): cu cât entropia, cu atât mai mare zona. Entropy ansamblu Y - al doilea oval cu o suprafață H (Y). În cazul în care benzile sunt independente statistic, și anume nu există nici o legătură între ele, ovaluri se intersectează. entropie completă a sistemului este suma entropiei, adică. E. Suma pătratelor.
În cazul în care are loc între relația ansambluri statistice (corelație), ovalele în cruce diagrama. Rezultată informații reciproce I (X, Y) și este o măsură cantitativă a acestei intersecție. Entropia scade cu cantitatea de informații:
Cu cât informația mutuală, relația mai strânsă, cu atât mai mică de entropie H (X, Y).
De la proprietate 5 entropie urmează
Comparând [5] și [2], observăm că expresia [5] caracterizează egalitatea reciprocă a informațiilor cu privire la banda X. dacă știi trupa au. și invers, cunoașterea ansamblului Y dacă X este cunoscut ansamblu.
Proprietățile informațiilor reciproce.
I (X, Y) ≤ min. Informarea reciprocă nu poate fi mai multe informații despre fiecare singur ansamblu.I (X, Y) ≤ min. Măsura logaritmică a fiecăreia dintre benzile separat, este mai mare sau egală cu informarea reciprocă.
7. Informația mutuală I (X, Y) are un maxim (distribuția de probabilitate este o funcție convexă).
Ne exprimăm informarea reciprocă deplină asupra probabilității de stări ale sistemului. Pentru a face acest lucru, vom scrie valorile de entropie a sistemelor individuale prin așteptarea:
Apoi expresia [6] devine
Expresia [8] transforma utilizând proprietățile matematice
așteptările sunt după cum urmează. Pentru un ansamblu de variabile aleatoare X poate defini o φ funcție (x) pentru toate valorile lui x. Aceasta stabilește o mapare X într-o multitudine de valori reale ale lui x. ansamblu
Acesta reprezintă un set de valori ale setului de variabile aleatoare. Pentru a calcula valoarea așteptată a lui y nu trebuie să cunoască py de distribuție (y) pentru probabilitățile y. Dacă px distribuție (x) peste ansamblul X este cunoscut,
Această formulă permite determinarea cantității totale de informare reciprocă cu privire la ansamblul X din numărul canalului de ieșire al ansamblului primit W. informație reciprocă se măsoară în biți.
Un model Markov sursă.
Luați în considerare o secvență aleatorie de orice număr de evenimente. În cazul în care elementele unei secvențe aleatoare - numere reale, aceste secvențe sunt numite procese stocastice. Numărul de element din secvența este interpretată ca momentul în care a apărut această valoare. În general, setul de valori de timp pot fi setate continuu sau discret de valori aleatoare poate fi, de asemenea, continuu sau discret
unde p (xi) - probabilitatea de apariție a xi în momentul i. Pentru a descrie acest proces este suficient pentru a indica p probabilitate (x) pentru orice x (probabilitate totală IHI- 1). Pentru a descrie mai multe modele de proces complex, trebuie să se bazeze pe proprietatea la starea de echilibru, care permite de a simplifica calculele matematice. Procedeul poate să fie staționar dacă, pentru orice n și t au ecuația
unde xi = x1 + t, i = 1, ... n. Un proces stocastic este staționar, dacă probabilitatea oricărei secvențe nu se schimbă atunci când se schimbă în timp. Caracteristici numerice, în special așteptarea proceselor staționare sunt independente de timp. Având în vedere procesele la starea de echilibru, putem calcula timpul independent de caracteristicile informaționale ale proceselor aleatoare. EXEMPLU proces staționar - un proces ale cărui valori sunt independente și identic repartizate.
Luați în considerare alt semnal care reprezintă o secvență de caractere, create de mesajele sursă discrete.
Shannon definește o sursă discretă a mesajului: „Putem presupune că o sursă digitală generează un caracter mesaj de caracter. El va alege caracterele consecutive, cu funcție de o anumită probabilitate, în general vorbind, la fel ca alegerile anterioare, și pe simbolul respectiv. Sistemul fizic sau un model matematic al sistemului care creează o secvență de simboluri definite de un anumit set de probabilități, numit proces probabilistic. Prin urmare, putem presupune că o sursă discretă este reprezentată printr-un proces aleator. Invers, orice proces aleatoriu care generează o secvență de simboluri discrete, alese dintr-un set finit poate fi privit ca o sursă discretă. "
Structura statistică a unui astfel de proces și proprietățile statistice ale sursei sunt complet determinate de p univariată (i), p bidimensional (i, j) probabilitățile de apariție a producției elementelor posturi sursă. După cum sa menționat, în cazul în care între elementele succesive ale mesajului nu există o relație statistică, structura statistică a mesajului este complet determinat printr-o combinație de probabilitate unidimensională. Aspectul unui element mesaj la ieșirea sursei poate fi privită ca un anumit eveniment, caracterizat prin probabilitatea lor de apariție. Pentru un set de evenimente, împreună cu lor a priori probabilități de apariție există un concept al ansamblului.
Exemple de surse discrete pot fi:
texte tipărite în diferite limbi.
Surse continue de mesaje care sunt convertite la digital folosind un proces de cuantificare (vorbire cuantificată, semnalul de televiziune.
3. Cauze matematice, atunci când sunt definite pur și simplu, în mod abstract un proces aleatoriu care generează o secvență de simboluri.
Asemenea surse creează o procese stocastice sunt cunoscute ca procese Markov discrete. In general, rezultatul poate fi descrisă după cum urmează. Există un număr finit de posibile „stări“ ale sistemului: S1, S2.Sn. Mai mult decât atât, există un set de probabilități de tranziție pi (j), r. E. Probabilitatea că un sistem în stare Si. apoi du-te la Sj de stat. Pentru a utiliza acest proces Markov ca origine a unui mesaj, doar trebuie să presupunem că la fiecare trecere de la un stat pentru a crea o literă la alta. Statul se va conforma cu „rămășița de influență“, precedat de literele. În exemplul grafic, „condiție“ este un punct nodal al circuitului, și probabilitățile de tranziție generate și astfel literele indicate la liniile corespunzătoare.
O astfel de sursă de patru litere A, B, C, B. având, respectiv, probabilitățile de tranziție de 0,1; 0,4; 0,3; 0,2, revenind la nodul după
creând scrisoarea următoare, se poate forma atât secvențe finite și infinite.
La sursă discretă poate fi extinsă caracteristici de semnal aleatorii, cum ar fi stationaritate și ergodicitate. Presupunând că sursa ergodic poate fi „... echivala valorile medii ale unor secvențe, împreună cu valoarea medie a ansamblului de posibile secvențe (diferența de probabilitate este egal cu zero).“ De exemplu, frecvența relativă a litera A în secvența infinită privată cu probabilitate unul va fi egal cu secvențele sale relative ansamblu de frecvență.
Cel mai simplu model de sursă care generează mesaje dependente este o sursa Markov. Un proces aleatoriu numit lanț Markovasvyaznostis, dacă există, și pentru orice n x = (x1, ..., xn) alfabet X, relațiile
Descriere proces Markov este dată de distribuția inițială de probabilitate pe secventele de valori ale primelor s și probabilități condiționate p (xn / xn-s, ..., xn-1) pentru toate secvențele posibile. Dacă aceste probabilități condiționate nu sunt modificate în timpul unei secvențe de timp de schimbare a lanțului Markov omogen se numește. Omogeni lanțului Markov conectat s = 1 se numește un lanț simplu Markov. Pentru a descrie este suficient pentru a indica p de distribuție a probabilității (x1) x aparținând setului X și probabilitățile condiționate
numitele probabilități de trecere ale lanțului Markov.
Probabilitățile de tranziție sunt convenabil scrise sub forma unei matrice pătratică de dimensiune M x M
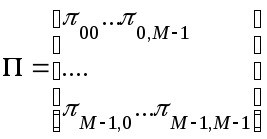
numita matricea probabilitate de tranziție. Această matrice - stocastică (non-negativ, elementele fiecărui rând este egal cu 1).
sau sub formă de matrice
Pentru un număr arbitrar de pași, vom obține n
,
t. e. probabilitatea de tranziție pentru n etapele pot fi calculate ca elementele matricei. Să presupunem că există un vector stohastic satisface ecuația
Stochastic vector p, care satisface ecuația [2], numit pentru distribuția staționară a matricei de tranziție lanț Markov definite prin Π. Distribuția finală de probabilitate este vectorul
Dimensiunea P∞ este independentă de distribuția inițială a timpului t. E. O distribuție staționară. Lanțuri, definite prin ecuația [3], numit ergodic. Dacă toate elementele matricei Π pozitive și nu este zero, lanțul Markov ergodic corespunzător. Pentru a formula condiția necesară și suficientă pentru ergodicitate, introducem unele definiții.
Continuitatea idostizhimo de la j de stat, în cazul în care pentru unii n probabilitatea de tranziție de la stat i să indice j în n etape este pozitiv. Setul de stări se numește închisă. în cazul în care nici un stat nu este C, nu se poate ajunge la starea în intrare C.
Lanțul se numește ireductibil. în cazul în care nu are seturi închise, în plus față de mulțimea tuturor statelor. Un lanț Markov este ireductibilă dacă și numai în cazul în care statul poate ajunge unul de altul. Statul i se numește periodică dacă există t> 1: că probabilitatea de tranziție de la i la i n trepte este egal cu zero pentru toate n nu este un multiplu T. Lanțul, care nu conține stări periodice se numește aperiodice. Nonperiodic ireductibilă lanț Markov ergodic.
1. C. Shannon, Funcționează pe teoria informației și cibernetica. M. Ed. "IL", 1963 pag 249 -. 259.