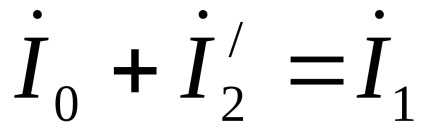Modul inactiv are loc în timpul funcționării transformatorului atunci când receptorul este oprit.
Transformator de curent înfășurare primară este oprit atunci când consumatorul de energie electrică este curent de mers în gol (
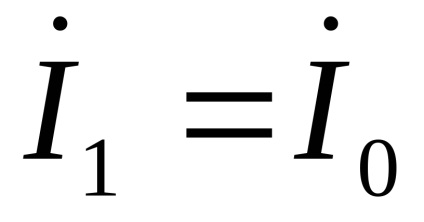
Unghiul inclus al magnetic ecuație pierdere (unghiul de fază dintre curentul și fluxul magnetic al transformatorului) se datorează pierderilor de putere în circuitul magnetic al transformatorului. Uglaobychno mică valoare pentru oțeluri electrice moderne este de 4 - 6.
tensiunea aplicată în timpul ralanti la un transformator, în conformitate cu a doua lege a Kirchhoff a înfășurării primare pot fi reprezentate ca suma:.
Pornind de la această ecuație, echilibrul electric, este posibil să se construiască o diagramă vector transformator pentru modul inactiv (Fig. 2).
atunci când devine necesar pentru a studia la ralanti transformator provedeniyaopyta. Acest test este efectuat pentru a determina coeficientul transformatsiin. potokaFm magnetic. factor de putere cosφ0. moschnostiPM și pierderi în miez a circuitului magnetic al transformatorului.
In experimentul de mers în gol la înfășurarea transformatorului primar este alimentat o tensiune egală cu valoarea sa nominală U1rated. înfășurarea secundară a transformatorului, astfel este deschis, deoarece nu este o sarcină pe circuit. Ca rezultat, curentul secundar este zero (I2 = 0). Conform înfășurarea transformatorului în aceste condiții primar, curentul curge hodaI0 inactiv. a cărei valoare este de obicei mică și a ordinului 410% din valoarea nominală a curentului în obmotkeI1NOM primar. Odată cu creșterea nominală de sarcină transformator de putere de curent scade relative de valoare.
Folosind a doua lege Kirchhoff pentru circuitele de transformare primară și secundară în modul inactiv, este posibil să se obțină următorul echilibru electric ecuația:
;
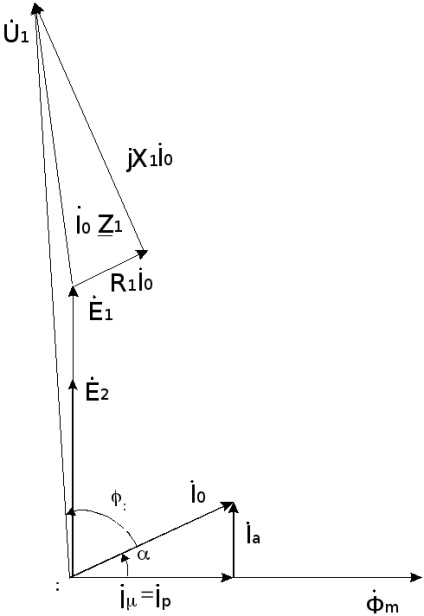
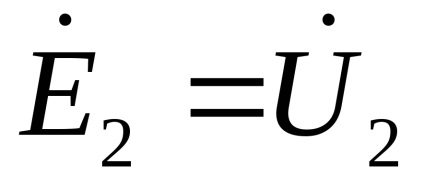
Neglijând influența căderea de tensiune pe înfășurarea a I0Z1 transformatorului primar. egală cu produsul de ralanti curent în rezistența primară obmotkiZ1 =

Puterea activă consumată de transformator de ralanti Px.x. cheltuit pentru pierderea puterii în pierderea de energie magnetică și electrică în primar: Px.x = Pm + PE1.
Deoarece rezistența R1 a înfășurării primare. precum și curentul fără sarcină a transformatorului hodaI0, pierderi de obicei ușoare, electrice în înfășurări sunt mici și pot fi neglijate. Ca urmare, se poate presupune că consumul de energie al transformatorului în experimentul de ralanti și măsurat prin wattmetru este consumat în pierderile magnetice cauzate de histerezis si curenti turbionari: Px.x = Pm.
Mod de încărcare transformator
operațiune de încărcare este o lucrare pentru transformatoare 1, 2 și 4 tipuri (vezi. clasificare) și este prevăzut la conexiunea la înfășurarea consumatorului de energie electrică secundar. În acest caz, circuitul de transformator înfășurare secundară este închis și sub alternativ deystvieme2 toki2 care curge prin circuit.
Valoarea curentă a curentului în înfășurarea transformatorului încărcat în conformitate cu legea lui Ohm secundar dat de expresia
,
unde ZPR =
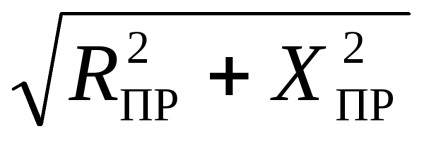
Deoarece rezistența înfășurării primare este mic, se poate presupune că aproximativ U1 E1. Din aceasta rezultă că, pentru o sursă de tensiune constantă (U1 = const) în modul de încărcare EDSE1 transformator poate fi considerat constant (E1 = const). Deoarece EMF induse rezultă un flux magnetic, apoi, în consecință, firul trebuie să rămână în mod substanțial constant la diferite (până la nominal) a sarcinii transformatorului t.e.F = const. schimbarea de sarcină conectată la bobina secundară, însoțită de o schimbare tokaI2. Aceasta determină o schimbare tokaI1 corespunzătoare. Transformator ca ajustează automat puterea energiei electrice transformată atunci când schimbă sarcina atașat la acesta. Aceasta este o proprietate foarte importantă de transformator nazyvaetsyasvoystvom de auto-reglementare.
Atunci când schimbările în amploarea și natura sarcinii transformatorului, de asemenea, se modifică și tensiunea la înfășurarea secundară.
La calculul circuitelor electrice cu sarcina de a calcula transformatorului este complicată din cauza cuplaj magnetic între înfășurările primare și secundare ale transformatorului. Această sarcină poate fi simplificată prin înlocuirea cuplajului magnetic electric. In acest studiu de caz modurile ce simplifică și reduce la calculele de circuit electric relativ simplu. Circuit electric în care cuplajul magnetic între înfășurările transformatorului este înlocuit cu un numit circuit echivalent electric.
Forma structura circuitului. Pentru acest pre face anumite transformări. Unind cele două înfășurări într-un transformator face un EMF egal al bobinelor (E1 = E2 „). Egalitatea va fi îndeplinită în cazul în care noul număr de rotații ale obmotkiw2 secundar „face egal cu numărul de rotații ale obmotkiw1 primare. t.e.w2 „= w1. Evident, pentru o astfel de transformare de editare toate cantitățile ce caracterizează circuitul secundar, și trebuie să recalculeze un nou număr de rotații. Valorile count circuitului secundar la noul număr de înfășurări ale circuitului secundar se numește acționarea la numărul de rotații ale circuitului primar, iar transformatorul în acest caz, se spune să fie redusă.
Pentru date ecuațiile de transformator care descriu fluxul de lucru în acesta, să ia forma:
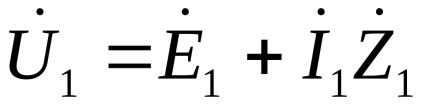
;
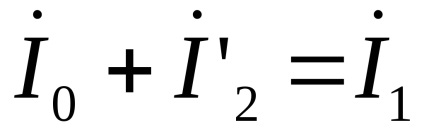
EMF

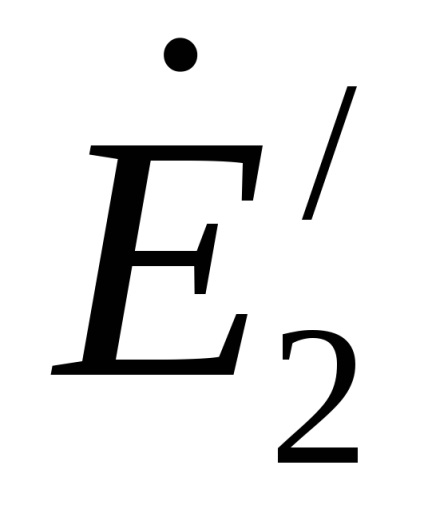
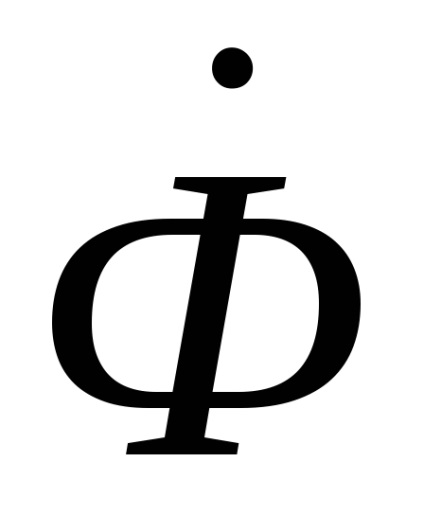
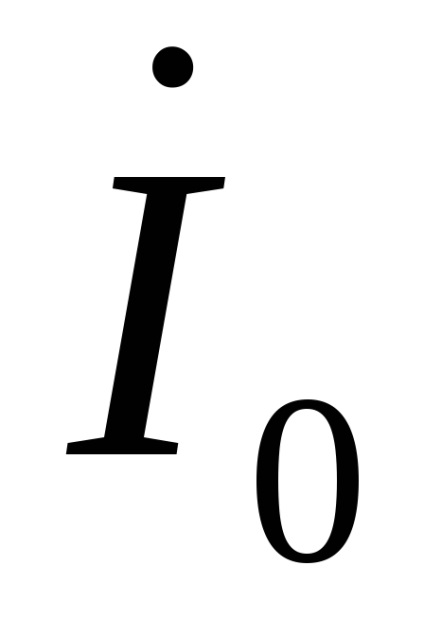
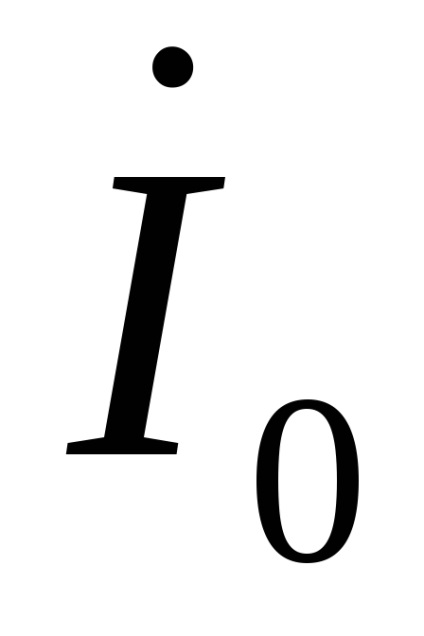
Acum, având în vedere ecuația de mai sus a completa starea electrică a înfășurărilor primare și secundare ale transformatorului dat să ia forma:
;
.
Pe baza acestor ecuații și că