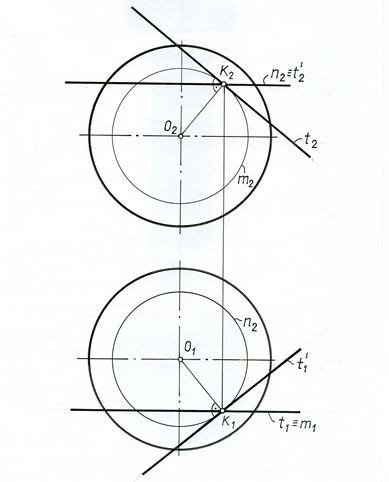
Problema 1. Construirea unui plan tangent la suprafața unei sfere în punctul K (Fig. 11.2).
Am ales două linii curbe care trece prin punctul C. Este recomandabil să se ia mai simplu grafic linii - cercul (paralele și meridiane) - n și m.
La aceste două cercuri de la un punct tangent la sârmă, în care în fiecare plan al circumferinței sale, adică T se află în verticală, și t „- în planuri orizontale.
tangentele Construit T și T „și specificați planul tangent dorit.
În această problemă, până la punctul - punctul de tangență eliptice. OK - raza este normal la planul tangent la punctul K. plan construit perpendicular pe acesta.
Problema 2. Construirea unui plan tangent la suprafața de rotație
la punctul K (Fig. 11.3).
Deoarece liniile care definesc planul tangent, să ia două
linii, dintre care una este tangent la un cerc - paralele, care trece prin punctul K, al doilea - tangenta la un meridian care trece prin același punct.
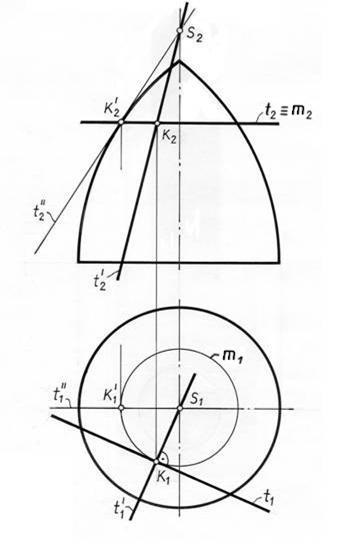
Pentru a desena o tangentă la meridianul, rotiți-l în sus
alinierea cu meridianul principal și trage tangent t „“ 2 în punctul
K'2. situată pe aceeași circumferință paralelă ca și punctul K până la intersecția cu axa de simetrie a cifrelor punctului S. După același punct S va avea loc tangent t „2 după revenirea pivotarea starea inițială meridian. Pentru al construi, conectați S2 și K2.
A doua tangentă t este construit în așa fel. proiecția ei frontală t 2 pe planul de proiecție frontală coincide cu proiecția circumferința paralelă m. Proiecția orizontală a t 1 este construit ca o linie tangentă la circumferința proiecției orizontale - m1 paralele.
Tangent T „și T“ și de a determina planul tangent necesar.
Rețineți că, în această problemă punct atinge K este, de asemenea, un punct de tangenta eliptică.
Problema 3. Construiți o tangentă la cilindrul de la punctul K (Fig. 11.4).
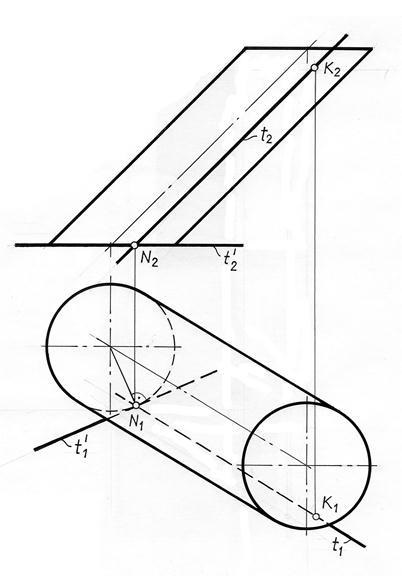
Element tangență plan pentru formarea cilindru cilindru va fi t. care se află la punctul K. În această sarcină, punctul atinge K este una dintr-o multitudine de puncte de atingere parabolice geometrice situate pe generatoarea cilindrului. Cu această primă generatoarea coincide t linia tangentă la suprafața.
A doua linie tangentă trece prin punctul N, care se află la baza cilindrului. Acest punct este un punct de intersecție cu planul t generatoarea baza cilindrului.
Construit linii tangente t și t „și formează un plan tangent la cilindrul de la punctul K.