
Deci, în răspuns la problema inițială, desigur, 2/3, deși majoritatea Internetului este responsabil de 1/2. Prima dată când selectați unul dintre cele 6 monede care sunt în cufere. În jumătate din cazuri, va fi de aur - adică, în trei cazuri (selectați al doilea aur al pieptului sau primul sau al doilea aur al treilea)! În două dintre aceste trei cazuri, selectați din aceeași monedă trunchi este de aur. Deci, răspunsul este: 2/3.
Amintind de Monty Hall. nu-i așa? Acum, ia în considerare generalizări ale problemei, pe care am inventat el însuși (cum ar fi, Internetul nu este prezent).
Tu N + 1 piept, fiecare este N monede. Total: N (N + 1) / 2 de monede de aur, aceeași cantitate de argint. Acestea sunt distribuite pe cufarele după cum urmează (a se vedea figura în cazul N = 5 ..):
Am ales una dintre aceste cufere la întâmplare și trageți orbește unul dintre monede. Este de aur. Care este probabilitatea ca a doua monedă, extrasă orbește din acest trunchi, de asemenea, de aur?

Surprinzător, răspunsul este independent de N! El întotdeauna 2/3!
Într-adevăr, moneda noastră se extrage aur - una dintre N (N + 1) / 2. Acesta nu poate fi primul trunchi. În cazul în care este a doua - șansa de a obține urme de aur sunt zero. Dacă este al treilea, șansele elimina urmele de aur - 1 / (N-1), etc. Considerăm că probabilitatea cerută este egală
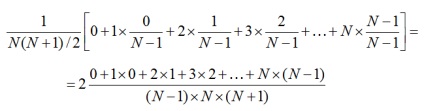
Rămâne să arate că numitorul este numărătorul, împărțit la 3, care este ușor de realizat prin inducție.
Personal, am acest fapt (că răspunsul este întotdeauna 2/3) uimit și amuzat. Într-un fel, se pare că odată cu creșterea N, probabilitatea trebuie să depună eforturi pentru a 1/2. Sau schimba cumva, pentru că problema inițială a fost exact 3 piept de 2 monede, astfel încât răspunsul este compus din 2 și 3 „nu doare ochii,“ și de ce este în cazul N-dimensional. Dar chiar mai mult intuitia mea ma condus la această generalizare:
Tu N + 1 piept, fiecare este N monede. Total: N (N + 1) / 2 de monede de aur, aceeași cantitate de argint. Acestea sunt distribuite pe cufarele după cum urmează (a se vedea figura în cazul N = 5 ..):
Am ales una dintre aceste cufere la întâmplare și trage orbește afară monede K (K Alexey Shramkov. Bună ziua. P (A | B) = P (AB) \ P (B) Pentru o anumită condiție a problemei de claritate, care este doar o singură alegere orb. Acest aranjament a problemei clasice cu ținta. Când facem o singură lovitură. Și pentru a determina probabilitatea de a lovi 10, dacă știm că ne-am lovit încă ținta. Șansa de a lovi undeva în obiectivul de 60%, iar probabilitatea de a lovi un 1-30%. Ai descrie alte sarcini. De fapt, tu te-ai scris și cum: Care este probabilitatea ca într-o ladă de monede de aur 2, cu condiția ca acesta are o monedă de aur. Această probabilitate - 1/2. Dar avem o întrebare: ce este probabilitatea de a extrage o a doua monedă de aur, după primul aur. Ie nu atât timp cât știm că există un aur (ne-ar arăta în portbagaj), și cu condiția ca ne-am scos o monedă de aur, și este în mâinile (aceasta este o alegere orb: știm că există deja a fost una de aur monede și nu știu nimic despre al doilea). De aceea, trebuie să ne amintim că de la ultimul piept pentru a scoate primul aur probabil decât al doilea. P (2 sol | sol 1) = F (ambele sol) / P (sol 1) P (2 sol | sol 1) = F (ambele sol) / P (sol 1) = (1/3) / (1/2) = 2/3 Alexey Shramkov. Alexander, mulțumiri pentru clarificare - pe deplin de acord cu rezultatul rafinamentul pe care „ceea ce probabilitatea de a extrage o a doua monedă de aur, după primul aur“, adică, în acest caz, putem scoate a doua monedă de la un alt piept. În formularea problemei confuz mine este că nu putem schimba selecția de piept după prima alegere orb, ci pur și simplu scoate restul de-a doua monede. „Care este probabilitatea ca a doua monedă în portbagaj - același aur?“ Nu, așteaptă un minut. Este ca și cum este scris, ceea ce probabilitatea de a extrage o a doua monedă de aur din același trunchi (I într-adevăr a însemnat implicit - a declarat în mod inutil în condiții). Formularea inițială este corectă - nu se schimba piept.
Unde sunt greșit în raționament? Răspunsul este de 50%, pare chiar de la datele brute.
B-eveniment în care, după selectarea unei monede trunchi> = 1 aur în ea
P (B) = 2/3.
Un eveniment în care, după selectarea pieptului = 2 monede de aur în ea
P (A) = 1/3
Problema este de a găsi probabilitatea unui eveniment A, B, după ce a avut loc evenimentul, și anume,
P (A | B) -?
A și B sunt evenimente dependente.
Probabilitatea de co-apariție a două evenimente dependente este produsul probabilității unuia dintre ei asupra probabilității condiționale a doua, calculată în condițiile în care a avut loc primul eveniment, și anume,
P (AB) = P (B) * P (A | B) => P (A | B) = P (AB) / P (B), unde P (AB) = P (A), eveniment inutil A investit în evenimentul B.
P (sol 1) = P (1 sol | 2a piept) R (trunchi 2d) + F (1 sol | al treilea trunchi) P (a treia trunchi) = 0,5 * 1/3 + 1 * 1/3 = 1/2articole similare