1. Bazele de desen de construire a unei teorii
1.1. tipuri de proiecție
În centrul construcției tuturor imaginilor, stabilite în geometrie descriptivă, sunt două metode de proiecție: centrale și paralele.
Dacă toate razele numite linii drepte proiectate sunt trase dintr-un punct S (centrul de proiecție), apoi
obținută în planul de proiecție P 0 imaginii subiectului este numită proiecția centrală.
De exemplu, proiecția centrală a obiectului (cutie) se obține după cum urmează: raze de dispariție puncte S, numit centrul de proiecție, se realizează un număr de raze prin punctul cel mai caracteristic al planului obiect la intersecția proeminențele c P 0 (Figura 1.1 a.).
Ca rezultat, vom obține imaginea obiectului, numit proiecția centrală. Această imagine este mărită, deoarece dimensiunea imaginii nu corespunde cu dimensiunea reală a obiectului. Prin urmare, proiecția centrală în desenele de inginerie care nu sunt utilizate.
Dacă razele punct (centrul S proiecție) mintea pentru a trece la infinit dispariție, obținem proiecția axonometrică a obiectului (fig. 1.1, b). La construirea proiecția axonometrică subiectul acesta din urmă este, de asemenea, situată în fața planul P 0. proiecțiilor proeminente raze dar realizate în paralel.

articole axonometrică da o clar, dar o imagine distorsionată a unui obiect: unghiurile drepte sunt convertite în ascuțit sau obtuz, un cerc - în elipse. Proiecția axonometrică tehnică se aplică numai în acele cazuri în care o imagine vizuală a obiectului.
Desenele inginerești sunt cele dreptunghiulare mai comune (ortogonale) proiecții, care sunt un caz special de proiecție paralelă. Proiectarea raze paralele fac cu planul de proiecție în unghi drept (de unde și numele „proiecția dreptunghiulară“).
Articol (fig. 1.1, c) un plan de proiecție frontală, astfel încât cele mai multe linii și suprafețe (de exemplu, muchii și fețe ale paralelipipedului) sunt paralele cu acest plan. Apoi, aceste linii și suprafețe vor fi reprezentate pe planul de proiecție într-o formă virtuală. În viitor, vom explora subiectul unei proeminențe dreptunghiulare.
1.2. CARACTERISTICI proiecție paralelă
1. Fiecare punct și linie în spațiul respectiv, sunt proiectate într-un punct pe o linie dreaptă (fig. 1.2).
2. O linie segment paralel cu planul (fig. 1.2), proiectată pe acest plan, în full-size (MN || M 1 N 1).
3. Proiecția segmentului nu poate fi mai mare decât intervalul (C 1 D 1 ≤ CD).
4. Dacă punctul aparține liniei, atunci proiecția punctului aparține acestei linii (fig. 1.3).
5. Dacă liniile sunt paralele, atunci proiecțiile lor sunt paralele între ele (fig. 1.3).
6. Raportul dintre segmente egal cu raportul dintre proiecția segmentelor (fig. 1.3), (Fallesa teorema).
7. Proiectarea formelor geometrice în mărime și formă nu se va schimba în plan deplasare paralelă de proiecție (fig. 1.4).
imagini de proiecție sunt utilizate atunci când efectuează desene, trebuie să îndeplinească următoarele cerințe de bază:
- să fie reversibil, adică astfel încât le era posibil să se facă un obiect descris;
- să fie vizual, adică astfel încât pe ele a fost posibil să se introducă subiectul;
- să aibă o construcție grafică relativ simplă.
│ A 1 = A × │ │ │ AA 2; │ A 2 = A x │ │ │ AA 1.
Revenind la desen complex, am pierdut modelul spațial, dar după cum vom vedea în continuare, acest desen oferă precizie și imagini udoboizmeryaemost probleme semnificative de construcții.
1.4. Proiecția unui punct pe cele trei planuri ale proiecțiilor
În practica de desen și în rezolvarea anumitor probleme, este necesar să se introducă un al treilea
plan de proiecție perpendicular pe cele două disponibile. Acest nou plan de proiecție notat P 3 și numitul plan profil de proiecție (fig. 1.6a). Trei avioane de proiecție împărți spațiu în opt octante care sunt numerotate în ordinea prezentată în Fig. 1.6, precum și. Ingineria desen curs atunci când obiectul de imagine este aranjat în Octant I-st.
Pentru formarea de desen complex combină P 1 și P 3 la planul P 2. Rezultatul este un desen trohproektsionny complex, de exemplu, punctul A, cu axele X Y și Z (fig. 1.6, b).
Segmente proeminente linii de la punctul A la planurile de proiecție sunt numite coordonatele punctului și sunt desemnate:
X A - abscisa; Y A - ordonata; Z A - applicate (Figura 1.6.).
În cazul în care coordonatele specificate ale punctului A (de exemplu, X A = 20 mm, Y A = 22 mm, Z A = 25 mm), atunci putem construi trei proiecții ale acestui punct (fig. 1.6, b).
1.5. Proiecția unei linii drepte și pozițiile sale diferite în raport cu planurile de proiecție
Linie - este un set de poziții succesive ale punctului de mișcare.
Direct - un fel de linie, punctul de mișcare care nu schimbă direcția de mișcare. Pentru construirea unei proiecții directe considera spațială modelul biplan complex desen (fig. 1.7, a).
proiecție dreptunghiulară a segmentului AB este construit după cum urmează: se omite perpendicularele din punctele A și B pe P 1 și P 2. planul obține proiecții orizontale respective ale A 1 și B 1 și proiecțiile frontale A 2 și B 2 din aceste puncte. Combinând linii drepte de proiecție, obținem proiecția orizontală și partea frontală dorită a segmentului AB. desen cuprinzător este prezentat în Fig. 1.7 b.
În plus față de dispozițiile generale, o linie dreaptă poate lua avioanele proeminențele următoarele dispoziții speciale:
a) linia dreaptă AB (h), paralel cu planul de proiecție orizontală P 1 - orizontal. orizontală proiecție frontală A 2 B 2 || OX. iar proiecția orizontală proiectată pe orizontală în mărime completă a segmentului A 1 B 1 =
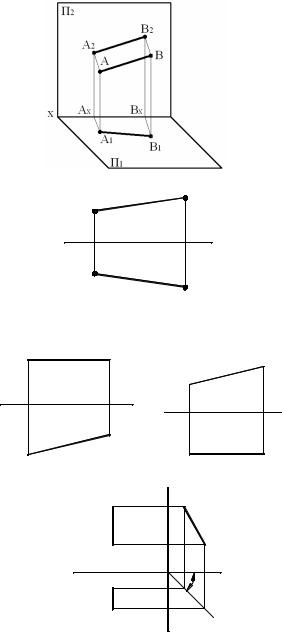
b) CD-ul liniei (f), paralelă cu planul frontal al proiecției P 2. numit frontal. Aici, C 1 D 1 -
În funcție de ce fel de avion acestea sunt perpendiculare proiecțiilor, liniile proeminente sunt:
a.) proeminente orizontal - AB P 1 (A 2 B 2 Fig 1.9 x, a). . B) proeminente frontally-- CD 2 n (C 1 x D 1 Figura 1.9, b).
c) proiectează profil - EF n 3 (E 2 F 2 F 1 z E y 1 figura 1.9 in) ....

1.6. Punct pe linia
Având în vedere un complex de desen linie directă generic AB (Fig. 1.10) și proiecție frontală a K (K 2) aparținând liniei. Apoi, proiecția orizontală a acestui punct aparține liniei AB. Acest lucru rezultă din proprietățile 4 (p. 7) proiecții paralele.
1.7. Proiecția unghiului drept
În abordarea una dintre sarcinile grafice operații geometrice de bază este de a efectua desen complex perpendicular pe linii drepte și suprafețe plane.
State fără dovezi teorema următoare proiectării unui unghi drept față de planul de proiecție: (. Figura 1.11), în cazul în care o parte a unghiului drept este paralelă cu planul de proiecție, iar a doua non-perpendicular pe acesta, apoi un unghi drept este proiectat pe acest plan, fără distorsiuni.