Proprietățile obținute din logaritmul stabilirii acesteia. Un fapt bine-cunoscut faptul că logaritmul b la bază și este definită ca exponent. doriți să ridice numărul de a, b pentru a obține numărul.
Obținem din modul de redactare a egalității evidentă 1 = 0 Loga, deoarece o 0 = 1 și, a = 1 Loga, deoarece o 1 = a.
Luați în considerare situația în care, în baza logaritmului argumentul sau în măsura necesară. Apoi, indicatorul acestui grad poate fi luat ca un semn al logaritmului următoarele reguli:
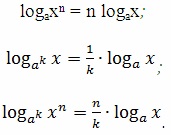
Desigur, toate aceste formule vor avea sens, în conformitate cu zona existentă a valorilor logaritmice. a> 0, a ≠ 1, x> 0. Și din nou, toate acestea pot fi utilizate nu numai de la stânga la dreapta, ci, dimpotrivă, și, prin urmare, a permis să se mute numerele cu care se confruntă logaritmului în sine logaritm. De fapt, acest lucru se face adesea.
Logaritmul gradului de numere pozitive este produsul indicelui gradului de baza sa de pe logaritm:
Sau, mai ușor, în acest caz, exponentul scos ca un factor. ca urmare a consumatoare de timp de schimbare de funcționare exponentiere la o operațiune de multiplicare mai elementar.
2) log7 49 6 = 6log7 49 = 6 · 2.
Pentru valori negative ale lui x formula devine fără sens. Astfel, este interzis să scrie log2 (- 4) 2 = 2log2 (- 4), ca expresie log2 (- 4) nu este definit. Cu toate acestea, rețineți că expresia de pe partea stângă a acestei formule, face încă un sens: