Luați în considerare un ABCD paralelogram, care are drept unghiul A.
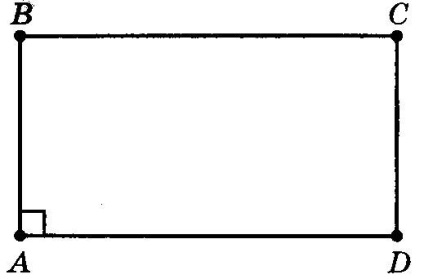
Prin proprietățile unghiulare care sunt adiacente de o parte, descoperim că unghiurile A și B împreună alcătuiesc 180 °. prin urmare,
Conform colțurile opuse ale proprietății paralelogramului poate fi scris:
Astfel, în cazul în care un unghi de un paralelogram liniei, apoi celelalte trei sunt de asemenea direct unghiul său.
Paralelogram, care are unghiul drept se numește dreptunghi.
Deoarece dreptunghiului este un paralelogram, atunci dreptunghiul are toate proprietatile unui paralelogram. Dar caseta are proprietăți speciale.
Înainte de a seta aceste proprietăți, ne amintim că cifra se numește axial simetrică în cazul în care, pentru fiecare punct al punctului figura axisimetric ea face parte, de asemenea, la această cifră. punctele axisimetrice se află la distanțe egale pe laturile opuse ale axei de simetrie pe aceeași perpendicular pe acestea. Figura de mai jos punctele A și A „și B și B“ axisimetric.
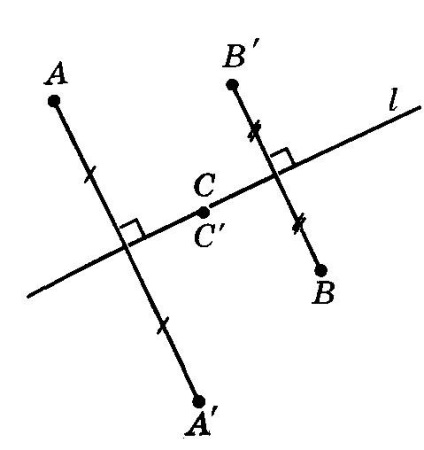
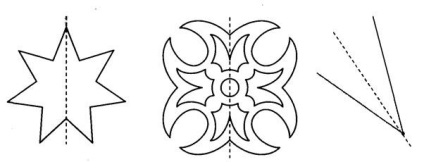
Dacă punctul C se află pe axa de simetrie l, atunci este simetric punctul C coincide cu punctul C. Figura de mai jos prezintă exemple de forme axisimetrice.
Luați în considerare PQRS paralelogram, ale căror laturi adiacente PQ și PS sunt egale. Deoarece partea QR, și PS, și PQ și SR sunt egale între ele ca părți opuse ale paralelogramului, se dovedește că paralelogramului PQRS toate laturile sunt egale.

Paralelogram, care are o pereche de laturi adiacente egal este numit un romb.
Prin definiție, un romb este un paralelogram. Din cauza rombul au toate proprietățile unui paralelogram.