
Acasă | Despre noi | feedback-ul
lichid de repaus relativ - echilibru lichid în vase care se deplasează în mod uniform accelerate vertical sau orizontal sau se rotește cu o viteză unghiulară constantă. În acest caz, forța de masă (gravitate) care acționează asupra lichidului se suplimentează forțele de inerție.
Formează suprafața liberă a lichidului la un echilibru relativ este o formă de suprafețe de presiune egală.
Ecuația suprafeței libere:
circulație verticală:
z = const - planul orizontal (1.5.1)
Pentru mișcarea orizontală:
z = (a / g) x + c - un plan înclinat (1.5.2)
și - accelerație, m / s 2;
Unghiul de înclinare a planului
a = arctg (- a / g); tg a = - a / g (1.5.3)
Pentru miscare de rotatie:
Z = zDespre + (v 2 r 2 / 2g) - un paraboloid de revoluție (1.5.4)
unde r - raza punctelor de rotație, m; v - unghiulara vitezei s -1;
zDespre - verticală coordonata vârful paraboloidului.
Creșterea presiunii în lichidul care se produce datorită rotației sale, este:
în care RO - presiunea la coordonatele Z = ZON și r = 0.
Volumul unui paraboloid de revoluție definită prin:
V = ½ n R 2 H, (1.5.7)
în care raza R a bazei paraboloidului; H - înălțimea.
NOTE LA REZOLVAREA PROBLEMELOR
Rezolvarea problemelor de acest subiect se bazează pe determinarea poziției libere suprafeței lichidului cu mișcare uniform accelerată. Alte obiective sunt la determinarea parametrilor geometrici ai secțiunilor transversale.
Exemplu 1.5.1 .Toplivny lungime rezervor L = 0,6 m, lățimea B = 0,5 m și o înălțime H = 0,2 m se deplasează cu o accelerație a = 3,27 m / s 2. Se determină cantitatea minimă de combustibil în rezervor pentru la intrare în conducta de benzină montat în mijlocul rezervorului la o înălțime h = 10 mm de fund.
Decizie. Cantitatea necesară de combustibil depinde de poziția suprafeței libere în timp ce se deplasează. Înălțimea punctului de prelevare benzină nu trebuie să fie mai mică decât înălțimea h.Po Formula (1.5.3) definesc panta suprafeței libere pentru mișcare uniform accelerată:
tg a = a / g = 3,27 / 9,81 = 0,333
Vom găsi distanța x:
x = h / tg a = 0,01 / 0,333 = 0,03 m
Din triunghiul găsim înălțimea h1:
h1 = [(L / 2) + x] tg a = (0,3 + 0,03) = 0,333 m 0,11.
Determinarea volumului de combustibil, volumul prismei triunghiulare:
Exemplul 1.5.3. Înălțimea vasului H = 0,3 metri este umplut cu lichid la un nivel h = 0,2 m. Pentru a determina ce w viteza poate învârti diametrul vasului D = 100 mm, că lichidul nu este stropit.
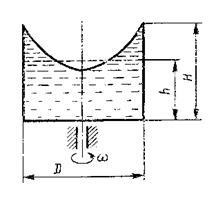
Noi luăm ca origine centrul de partea de jos a vasului, apoi coordonata Z = H.
ZO vertex coordonate rotație paraboloid găsi volume egale de corp lichid și umplut de revoluție: V = vm:
Volumul de umplut lichid V = h p R 2 volumul .ca al corpului de rotație este compus din înălțimea lichidului volum ZO și volumul înălțimii lichidului (H - ZO) minus valoarea de rotație a paraboloidului definit prin Formula (1.5.7), și anume:
Asimilarea laturile din dreapta, obținem
h p R2 = (ZO p R2) + [(N - ZO) p R 2] - [(N - ZO) p R 2/2]
După reducerea (p R 2), obținem h = ZO + H - ZO - [(N - ZO) / 2]
În cazul în care ZO = 2h - 2. H = 0.2-.3 = 0.1m
Am găsit viteza unghiulară