Teorema. Fie p 1 si p 2 - oricare două linii oblice. Dacă luăm în considerare toate posibile A1A2 directe. astfel încât A1 se află pe linia p 1. și A2 se află pe linia p 2. următoarele două afirmații sunt adevărate:
- Dintre toate liniile A1A2 există o linie dreaptă unică perpendicular pe linia p 1 și p 2 la linia (comune perpendicular pe cele două linii oblice).
- Dintre toate segmentele de lungime segment A1A2naimenshuyu este comun perpendicular pe cele două linii oblice.
Dovada. Demonstrăm mai întâi existența comune perpendicular pe cele două linii oblice.
Printr-un p punct 1 linie arbitrar trage o linie paralelă cu linia 2. p și printr-un punct arbitrar p 2 linii trage o linie paralelă cu linia 1. Vom nota cu avionul p α trece prin calea cea dreaptă p 1, iar litera β plan care trece prin p dreaptă și 2 (Figura 1).
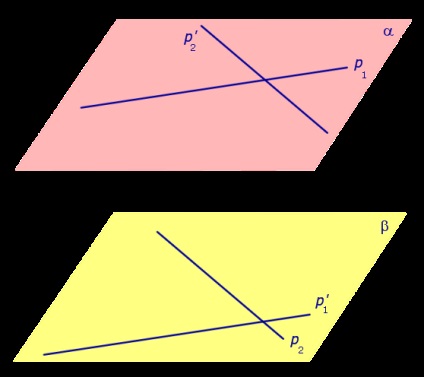
Deoarece linia 1 paralelă cu o linie dreaptă p situată în planul β. pe baza paralelismului liniei drepte și planul paralel cu planul p p 1. În mod similar, deoarece linia dreaptă este paralelă p 2. situată pe planul p. pe baza liniei drepte și planul paralel paralel cu planul p. Astfel, planul cuprinde două linii de subunitatea p intersectate 1 și p plane paralele. Prin caracteristica de planuri paralele, concluzionăm că avionul a și p sunt paralele.
Proiectam dreaptă p 1 plan β. Obținem drept, care este proiecția unei linii drepte 1. p și reprezintă punctul de intersecție al liniilor și litera p 2 B2 (fig. 2).
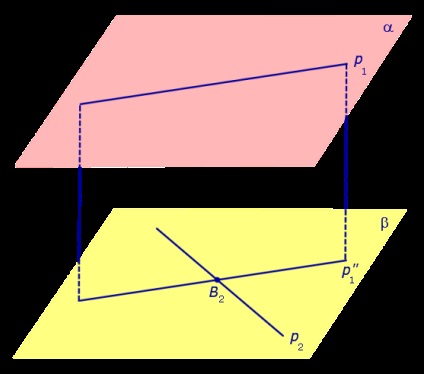
Acum proiect linia 2 p pe planul a. Obținem drept, care este proiecția unei linii drepte 2. p și reprezintă punctul de intersecție al liniilor de p 1 și B1 literă (Fig. 3).
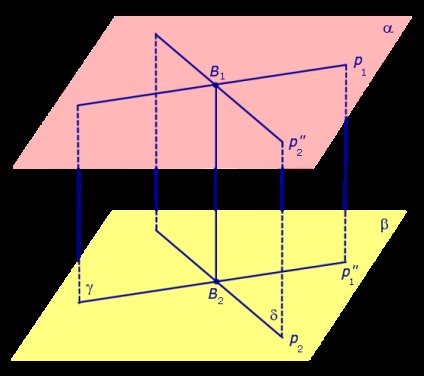
Deoarece punctul B2 este punctul de proiecție B1. avioanele liniei B1B2 perpendiculare fiecare dintre α și β. Prin urmare, B1B2 linie și perpendicular pe fiecare dintre liniile p 1 și p 2 .tak manieră, B1B2 - comun perpendicular pe liniile oblice p 1 și p 2.
Dovada existenței comune perpendicular pe cele două linii oblice este finalizată.
Arătăm că B1B2 linia construită este singura comună perpendicular pe liniile p 1 și p 2.
Rețineți că orice linie dreaptă perpendicular pe p 1 și p pe bază 2. linia perpendiculară și planul este perpendicular pe planurile a și p construite deasupra (fig. 3). Mai mult decât atât, totalul perpendicular pe liniile p 1 și p 2 ar trebui să treacă printr-un punct care se află pe linia 1. p și deci aceasta trebuie să se situeze într-un plan perpendicular γ. perpendicular pe planurile a și β. și trecând prin linia p 1.
Astfel, totalul perpendicular pe liniile p 1 și p 2 este intersecția dintre planele γ și δ, adică B1B2 drepte.
Dovada unicității comune perpendicular pe cele două linii oblice este finalizată. Aserțiunea 1 este demonstrată.
Să ne întoarcem la dovada Propoziția 2. Pentru aceasta considerăm un segment de linie A1A2 arbitrar. A1 al cărui capăt se află pe planul a. se încheie și A2 se află pe un plan β. A1 omite perpendicular dintr-un punct de pe plan p și baza perpendicularei notat cu simbolul A3 (Fig. 4).
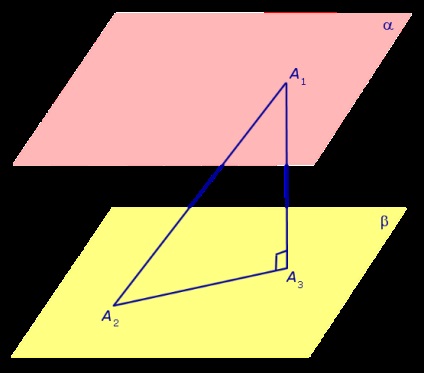
Dacă A1A2 nu este tăiată perpendicular pe planurile a și β, punctul A3 coincide cu punctul A2. și triunghiul A1A2A3 este un triunghi dreptunghic cu ipotenuza și A1A3 piciorul A1A2. De la dreapta lungimea piciorului triunghi mai mică decât lungimea ipotenuzei, atunci