Cuvântul „inferior“ înseamnă că înălțimea barierei este mai mică decât energia particulelor (fig. 4.12).
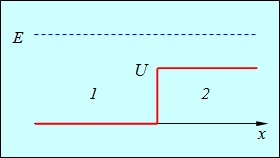
Fig. 4.12. Bariera potențial scăzut: linia punctată arată energia particulei incidente pe partea stângă,
cifre număr de zone cu diferite de energie potențială
Noi rezolva ecuația Schrödinger separat pentru fiecare dintre domeniile. In regiunea 1 energia potențială este zero, și obținem aceeași ecuație (4.22), care pentru o particulă liberă, iar soluția generală în forma deja cunoscută
și în care - amplitudinea incidentului și undele reflectate respectiv.
În regiunea 2 a ecuației Schrödinger este
În acest domeniu, se schimbă energia cinetică (și impulsul) unei particule, și trebuie să introducem un alt vector de undă (notat față de cel dintâi)
Apoi, este evident că în zona 2, soluția ecuației Schrodinger va avea aceeași formă ca și pentru regiunea 1 cu înlocuire. Cu toate acestea rezultă din considerente fizice care în regiunea 2 nu poate fi un val de înmulțire de la dreapta la stânga (punctul de la infinit din care nu este reflectată). Prin urmare, funcția de undă în această regiune corespunde undei directe
De fapt, aici, din nou, am folosit un fel de condiție de frontieră, deși altfel decât pentru stat legat. Rămâne doar pentru a determina amplitudinea undelor.
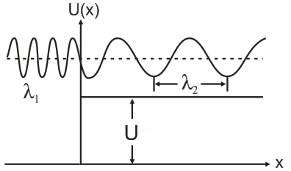
Fig. 4.13. Natura schematică a funcției de undă a particulei pentru cazul unei bariere potențial scăzut
Pentru a face acest lucru, trebuie să ne amintim că și - valoarea uneia dintre funcției de undă în diferite regiuni spațiale. Această funcție de undă trebuie să fie continuă, împreună cu primul său derivat în raport cu x. Continuitatea funcției în punctul x = 0 înseamnă că condiția trebuie să fie îndeplinite
Continuitatea primei derivate a funcției de undă este egalitatea
Soluție două ecuații care rezultă dă
Amplitudinea undei incidente este incert: este clar că aceasta depinde de intensitatea fluxului de particule! Ceea ce contează nu este amplitudinea, iar raportul R al pătratelor valorilor lor absolute, adică intensitățile undelor reflectate și de incidente,
Magnitudinea R se numește coeficientul de reflexie al particulelor dintr-o barieră joasă. In sensul fizic este probabilitatea particulelor de reflexie de barieră. În consecință, valoarea
numitul coeficient de transmisie, determină probabilitatea de penetrare a particulelor în zona din dreapta. Surprinzător, particula are o șansă de a fi reflectată de o barieră scăzută și să se întoarcă înapoi. În fizica clasică, o particulă este întotdeauna (R = 0) devine peste bariera dacă acesta este suficient pentru această energie. De exemplu, din punct de vedere al fizicii clasice, cu o energie de electroni de 10 eV. a pierdut condensator întârziind câmp B 5 eV. depăși cu siguranță, inhibarea și să continue să avanseze cu o energie redusă de 5 eV. În teoria cuantică, cu toate acestea, este non-zero, probabilitatea ca electronul se va reflecta din domeniul condensatorului și să se întoarcă înapoi. Reflectanta poate fi măsurată prin direcționarea unui flux de particule pe barieră și măsurarea proporției particulelor reflectate din ea.
Bariera de mare fără sfârșit
Energie potențială este de același tip, dar înălțimea barierei de energie particulelor mai mici: <(рис. 4.14).
Fig. 4.14. barieră potențial ridicat
Soluția pentru 1 rămâne aceeași: o suprapunere a undelor directe și reflectate. În regiunea 2 datorită relației inverse dintre energia particulelor și înălțimea barierei vectorului de undă devine imaginar:
Prin substituirea unui vector val imaginar
în expresia (4.32) pentru a obține reflecție coeficient R care R = 1. Ca și în clasic, cu energia particulei, de barieră infinit înălțime mai mică reflectată sigur de ea. Cu toate acestea, în fizica clasică, o particulă nu penetrează bariera. Soluția noastră la ecuația Schroedinger pentru regiunea 2, în cazul de mare obstacol devine
Acesta nu este un val, și funcția exponențială descompunere. Ca și în cazul barierei scăzută aruncate soluție nonphysical - creștere exponențială funcție a formei
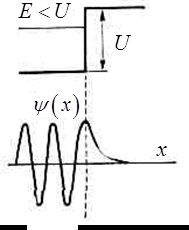
Fig. 4.15. Natura schematică a funcției de undă a unei particule în cazul barierei potențial ridicat
Adâncimea de penetrare a barierei de particule conform înțelege distanța pe care debitul (probabilitate) se diminuează în timp e. Din expresia rezultă că
Potențiala bariera de lățime finită
Energia potențială este dată de
Primirea am omis o serie de factori înainte de exponent că sensul fizic înseamnă a neglija procesele atunci când particula înainte de a ieși de sub bariera pentru a experimenta multiple reflecții din pereți. La contribuție ridicată și la nivel de barieră a unor astfel de procese este mic și a făcut apropiere este justificată.
Devine negativ. Cazul de salvare relația de incertitudine. Modulul (imaginar) al vitezei particulelor este de ordinul
astfel încât timpul de tunelare
Incertitudinea în energia cinetică
Din rezultatele obținute pentru coeficientul de transmisie se poate observa că efectul de tunel este vizibil dacă
Se pare că incertitudinea în energia cinetică a particulelor sub o barieră mai mare decât valoarea energiei cinetice. Prin urmare, este imposibil să se argumenteze că sub bariera de energie cinetică este negativ. Mai degrabă, este „neclară“, astfel încât particula ar putea dori să sară o barieră prea mare. În cazul unei bariere „neclaritate“ mai mare și mai largă a energiei cinetice trebuie să fie foarte mare, ceea ce este posibil numai pentru un timp foarte scurt, în timpul căreia a particulelor nu poate aluneca peste bariera. Prin urmare, în acest caz, factorul de transmisie devine exponențial scăzută. Într-un alt mod: bariera de tunel vizibile atunci când ordinea lățimea a lungimii de undă a de Broglie.
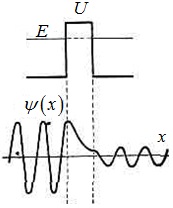
Fig. 4.17. Funcția de undă a unei particule în cazul barierei de potențial finit
Bariera de formă arbitrară poate fi reprezentată ca o serie de bariere dreptunghiulare; Teorema de multiplicare a probabilităților conduce la suma (integrală) în exponent, astfel încât în loc de (4,34) avem