În teoria probabilității, punerea în aplicare a unui set de condiții de testare numite. Rezultatul testului, detectat ca un fapt, se numește un eveniment.
suna Randomly eveniment care, ca urmare a poate să apară testul sau nu pot să apară (spre deosebire de un anumit eveniment, care, în punerea în aplicare a acestui complex vine întotdeauna, iar evenimentul imposibil care are loc niciodată în punerea în aplicare a acestui set de condiții). O descriere completă a unui eveniment aleator este probabilitatea apariției acestora. Exemple de evenimente aleatoare sunt eșecurile în sistemele economice; volumele de producție ale fiecărei companii în fiecare zi; Ratele de schimb în birouri de schimb valutar; starea de piață a valorilor mobiliare și de afaceri de schimb, și așa mai departe. n.
Simularea de evenimente aleatoare este de a identifica ( „trage“), faptul care sa produs.
Pentru a simula evenimentul aleatoriu A, care vine în experimentul cu RA probabilitate, doar o singură întâmplare (o pseudo-aleatoare) numerele R, repartizate uniform pe intervalul [0; 1]. În cazul PN R care se încadrează în intervalul [0; RA] evenimentul A este considerat a fi avut loc în acest experiment; în caz contrar - nu va veni în acest experiment. Fig. 10.5 prezintă cele două rezultate posibile: dacă evenimentul R1 pSCH trebuie considerate a fi produs; atunci când evenimentul PN R2- în acest studiu nu a venit.
Este evident că este mai mare probabilitatea de apariție a evenimentului simulat, mai pSCH, uniform distribuite pe intervalul [0; 1], va cădea în intervalul [0; RA], ceea ce înseamnă că faptul de apariție a evenimentelor din proces.
Pentru simularea unui grup complet incoplete evenimente aleatoare N A 1, A 2. O sveroyatnostyami PA1 apariție, PA2,. PAN> respectiv ca un singur PN R.
Pentru pot fi înregistrate astfel de evenimente aleatoare
Faptul de apariție a unuia dintre grupul de evenimente este determinată pe baza condițiilor de aderare pSCH R un slot special, care împart intervalul [0; 1]. De exemplu, în Fig. 10.6 pSCH R1 să creadă că vin 2. Dacă evenimentul A pSCH a fost egal cu R2, considerăm că a avut loc evenimentul A (N - 1).
În cazul în care evenimentul nu este un grup complet administrat suplimentar (inactiv) Eveniment A (N + 1), a căror probabilitate este dată de:
Mai mult, există deja stabilite de algoritmul pentru grupul plin de evenimente cu o modificare: în cazul în care PN devine ultima (N + 1) lea interval, consideră că nici unul dintre evenimentele N care fac un grup incomplet, nu a venit.
În practica studiilor de simulare este adesea necesar pentru a simula evenimente dependente, pentru care probabilitatea unui eveniment este dependentă de faptul dacă sunt sau nu pot avea loc un alt eveniment. Ca un exemplu de evenimente dependente da livrarea bunurilor către consumator, în două cazuri: atunci când traseul de circulație este cunoscută și a fost furnizorul în continuare rafinat și mai precis când traficul de marfă a fost efectuat. Este clar că probabilitatea de livrare de la furnizor la consumator pentru un anumit caz va fi diferit.
Pentru a simula două independente aleatoare evenimente A și B, trebuie să setați următoarele probabilități complete și condiționate:
Rețineți că, dacă probabilitatea de apariție a unui eveniment în condiția ca evenimentul A nu a venit, nu este specificat, acesta poate fi definit prin formula
Există doi algoritmi pentru modelare evenimente dependente. Una dintre ele poate fi numită „modelare consistentă“; o alta - „Modelarea după calcule preliminare.“
Modelarea consecventă. Algoritmul de simulare secvențială este prezentată în Fig. 10.7.
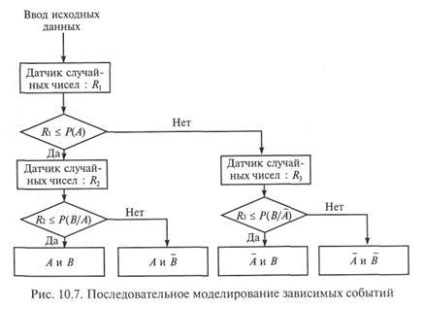
Avantajele neîndoielnice ale acestui algoritm sunt simplitatea și naturalețea ca evenimente dependente „jucat“, seria - așa cum apar ele (sau nu apar) în viața reală, care este o trăsătură caracteristică a majorității modelelor de simulare. Cu toate acestea, algoritmul oferă o referință de trei ori la un generator de numere aleatoare, care crește timpul de simulare.
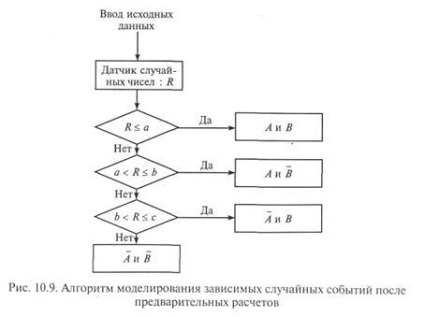
Modelarea după calcule preliminare. După cum puteți vedea, sunt prezentate în Fig. 10.7 patru evenimente dependente de rezultatul de simulare formează un grup complet de evenimente care se exclud reciproc. Aceasta se bazează pe algoritmul de simulare, oferind un calcul preliminar al probabilităților fiecărui rezultat și „trage“ faptul apariției unuia dintre ei, ca și pentru orice grup de evenimente care se exclud reciproc. Fig. 10.8 ilustrează un interval de divizare [0; 1] pe cele patru segmente, a căror lungime corespunde rezultatului probabil al evenimentelor.
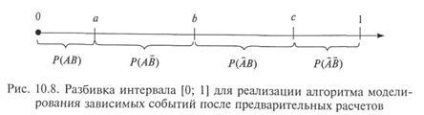
Fig. 10.9 conține algoritmul de simulare. Acest algoritm oferă un singur apel la un generator de numere aleatoare, care oferă în timp câștig de simulare în comparație cu simulare secvențială, dar înainte de începerea cercetătorului algoritm trebuie să calculeze și să intre probabilitatea tuturor rezultatelor posibile (desigur, această procedură simplă, puteți desena în software-ul, dar mai multe algoritm lungesc).