Detectoarele și proprietățile lor, determinanții de calcul on-line. Permutare a numerelor 1, 2. n este orice aranjament al acestor numere într-o anumită ordine. In algebra elementară se dovedește că numărul de permutări care pot fi formate din n numere egal cu 12. n = n. De exemplu, din cele trei numere 1, 2, 3 pot forma un 3 = 6 permutare: 123, 132, 312, 321, 231, 213. Se spune că, într-o anumită permutare a numerelor i și j reprezintă inversiune (tulburare) dacă i> j dar ar trebui să i în această rearanjare înainte de j, atunci în cazul în care există un număr mai mare de costuri mai mici din stânga.
Permutare se numește chiar și (sau impar). în cazul în care chiar și, respectiv, (nui adevărat) numărul total de inversiuni. Operațiunea prin care de la o trecere la alta permutare compusă din același număr n, numit gradul-podstanovkoyn lea.
Schimbare care transformă un permutare la altul, este înregistrată în două rânduri în paranteze comune, numărul care ocupă același spațiu în aceste permutări sunt denumite adecvate și scrise unul sub altul. De exemplu, simbolul reprezintă substituția în care comutatoarele 3 4 1 2 ®, ® 1 2, 3. 4 ® Substituire numit chiar (sau impare), în cazul în care numărul total de inversiuni în ambele rânduri de substituție este chiar (nui adevărat). Orice permutare de gradul n-lea pot fi scrise sub forma, de exemplu. cu un aranjament natural al numerelor pe linia de sus.
Să presupunem că avem o matrice pătratică de ordinul n
Luați în considerare toate produsele posibile de n elemente ale acestei matrici sunt luate unul câte unul și numai unul din fiecare rând și fiecare coloană, adică produse de forma:
în cazul în care indicii q1, q2. Qn constituie o permutare a numerelor
1, 2. n. Numărul acestor produse este numărul diferitelor permutări de n simboluri, adică, egal cu n. Semn al produsului (4.4) este egal cu (- 1) q, unde q - numărul de inversiuni din permutarea indicilor doua elemente.
Determinantul de ordinul n-lea corespunzătoare matricei (4.3) se numește suma algebrică a n! termeni de forma (4.4). Folosit pentru înregistrarea caracterelor sau det determinant A = (determinant sau determinant al matricei A).
Proprietățile determinanților
1. Determinantul nu se schimbă dacă vă transpune.
2. Dacă unul dintre rândurile de determinant constă din zerouri, determinantul este zero.
3. În cazul în determinantul rearanja două rânduri, modificările determinante semnează.
4. determinant care cuprinde două rânduri identice dispare.
5. În cazul în care toate elementele unui rând de determinantului se înmulțește cu un numar k, factorul determinant în sine înmulțit cu k.
6. determinant care cuprinde două linii proporțională este zero.
7. În cazul în care toate elementele i-lea rând de determinantului exprimat ca sumă a doi termeni ai j = bj + cj (j =), atunci determinantul este egal cu suma determinanților pentru care toate rândurile cu excepția i-lea - cum ar fi într-un predeterminat determinant, și rândul i-lea într-una dintre componentele constă din elemente BJ. într-un alt - a elementelor cj.
8. nu se schimbă determinant dacă elementele de una dintre liniile sale sunt adăugate elemente corespunzătoare ale unui alt rând înmulțit cu același număr.
Notă. Toate proprietățile rămân valabile în cazul în care în loc de șiruri ia coloanelor.
Minor Mi elementul j determinant ai j d ordine n-lea este determinantul de ordinul n-1, care se obține din d ștergerea rândului și coloanei care conține elementul activ.
Cofactor al elementului ai j d este factorul determinant al lui Minor Mi j. luate cu semnul (-1) i + j. Cofactor al elementului ai j va fi notat cu Ai j. Astfel, Ai j = (-1) i + j Mi j.
Metode de calcul practic determinanților care se bazează pe faptul că determinantul de ordinul n poate fi exprimată în termeni de determinanți ordinele mai mici date de teorema următoare.
Teorema (extinderea determinantului de-a lungul unui rând sau coloană).
Factorul determinant este suma produselor tuturor elementelor din oricare din rândul său (sau coloana) de către cofactori lor. Cu alte cuvinte, există o descompunere a elementelor d ale rândului i-lea
sau coloană -j th
În special, în cazul în care toate elementele rând (sau coloana), cu excepția unuia singur, egal cu zero, determinantul este acel element înmulțit cu cofactor acestuia.
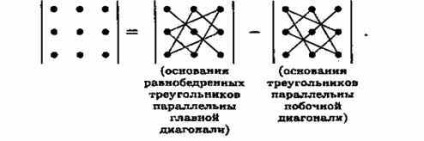
Formula de calcul determinant al treilea ordin.
Pentru a facilita memorarea formulei:
Exemplul 2.4. Fără a calcula determinant. arată că este egal cu zero.
Decizie. Scădeți din rândul al doilea obține primul determinant. egală cu originalul. În cazul în care un al treilea rând și scade primul, veți obține determinant. în care cele două linii sunt proporționale. Acest factor determinant este zero.
Exemplul 2.5. Se calculează determinanți D =. extinderea prin elementele din a doua coloană.
Decizie. Extindem determinantul de elementele din a doua coloană:
Exemplul 2.6. Calculați determinantul
în care toate elementele de pe o parte a diagonalei principale sunt egale
Decizie. Extindem determinant al A prima linie:
Determinantul de picioare pe dreapta, poate fi re-extins, în primul rând, obținem:
Și așa mai departe. După n pași pentru a ajunge la ecuația A = a11 a22 .. ann.
Exemplul 2.7. Calculați determinant.
Decizie. În cazul în care fiecare rând de determinant, din moment ce al doilea, se adaugă prima linie, veți obține un factor determinant în care toate elementele care sunt sub diagonala principală sunt zero. Și anume, obținem determinantul :. egală cu originalul.
Procedînd ca în exemplul anterior, am găsit că este egală cu produsul elementelor diagonale, adică n. Metoda prin care determinantul calculat, metoda este chemat să aducă formă triunghiulară.
Calculul determinanților on-line
Introduceți detaliile și faceți clic