1 °. Determinarea derivatelor parțiale.
Să o z funcție = f (x, y). Deoarece x și y - variabile independente, una dintre ele poate fi schimbată, iar cealaltă pentru a păstra valoarea lor. Dăm variabilă independentă x creștere; menținerea valorii neschimbate y. Apoi, z este incrementat, care este numit prirascheniemz privat lui x și se notează. Astfel,
În mod similar, obținem parțială increment z la y:
Funcția increment completă definită de ecuația z
În cazul în care există o limită
aceasta se numește derivata parțială a funcției z = f (x, y) la punctul M (x, y) în variabila x și se notează cu un simbol:
Derivatele parțiale ale lui x; Mo în punctul (x 0, y 0) este în general notat cu simboluri
Acesta este definit în mod similar, și este notat derivata parțială z = f (x, y) în y:
Astfel, derivata parțială a unei funcții a mai multor (două, trei sau mai multe) variabile este definit ca un derivat al uneia dintre aceste variabile valori constante furnizate ale variabilelor independente rămase. Prin urmare, derivatele parțiale ale funcției f (x, y) sunt formulele și regulile de calculare a derivaților unei variabile (x sau y, respectiv, considerată constantă).
Exemplu. Găsiți derivatele parțiale ale
Exemplu. Găsiți derivatele parțiale ale funcțiilor.
Decizie. Având în vedere y ca o valoare constantă, obținem:
În mod similar, considerând x. ca o constantă, avem;
2 °. Teorema lui Euler. Funcția f (x, y) este numit omogen funcție de măsurare n. dacă pentru orice ecuație k reală multiplicator deține.
Funcția rațională Întreaga este omogenă dacă toți membrii săi aceleași modificări. . Pentru omogen diferențiabilă funcția de măsurare f satisface relația (teorema Euler):
3 °. Sensul geometric al derivatelor parțiale ale unei funcții de două variabile.
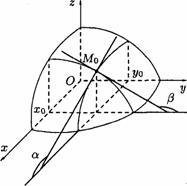
Graficul funcției z = f (x, y) este o suprafață. Funcția Schedule z = f (x, y0) este linia de intersecție a acestei suprafețe cu planul y = y0. Bazat pe sensul geometric al derivatului pentru funcțiile unei variabile, putem concluziona că. unde a - unghiul dintre axa x și tangent la curba z = f (x, y0) la punctul Mo (x0; y0; f (x0, y0)) (figura 8.).
4 °. derivați de ordin superior
Derivații parțiale se numesc prim ordin derivate parțiale. Ele pot fi considerate ca funcții (x; y) Î D. Aceste funcții pot avea derivate parțiale, care sunt numite ordinul al doilea derivate parțiale. Acestea sunt determinate și identificate după cum urmează:
In mod similar sunt definite derivate parțiale a 3, 4 și t. D. Ordinele.
Derivatul parțial al doilea ordin sau mai mare, luate pe diferite variabile se numește un derivat parțial amestecat. Acestea sunt, de exemplu,
Exemplu. Găsiți al doilea ordin derivatele parțiale ale funcției
z = x 4 - 2x 2 y 3 + y 5 + 1.
Acest rezultat nu este intamplatoare. Există o teoremă, pe care am stat fără dovezi.
Schwartz teoremă. Dacă derivatele parțiale de ordin superior sunt derivați continue, amestecate de același ordin, care diferă doar în ordinea de diferențiere, sunt egale.
În particular, pentru z = f (x, y), avem: