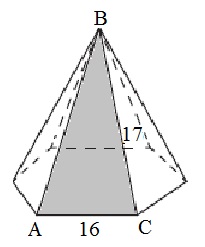
Parte a bazei piramidei hexagonală regulată sunt 16, laterale egale marginile 17. Găsiți aria suprafeței laterale a piramidei.
Deoarece piramida este corectă, apoi la baza unui hexagon regulat, atunci toate bază sunt interconectate și suprafața laterală a piramidei este format din șase triunghiuri isoscele egale ale căror baze 16 și partea - 17.
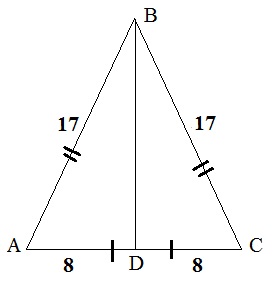
Pentru a găsi începutul zonei de o față laterală. Pentru aceasta considerăm isoscel ABC triunghi (a se vedea. Figura de mai jos). Știm că aria unui triunghi isoscel este egală cu produsul dintre înălțimea jumătate din lungimea bazei $ S = \ frac \ cdot un \ cdot h $. Lungimea bazei, știm că trebuie să găsiți înălțimea.
În triunghiul ABC, știm bază, este 16. Desenați înălțimea la baza ca un triunghi isoscel, inaltimea este mediana, apoi se împarte în jumătate de bază. Prin urmare, AD = DC = 8. Conform teoremei lui Pitagora, vom găsi înălțimea BD:
\ [AB ^ = BD ^ + AD ^ \]
\ [17 ^ = ^ BD + 8 ^ \]
\ [BD ^ = 225 \]
\ [BD = 15. \]
Acum substitui valorile numerice în formula pentru a găsi zona unui triunghi isoscel:
\ [S = \ frac \ cdot 15 \ cdot 16 = 120. \]
Anterior, a scris că suprafața laterală a piramidei este format din șase triunghiuri isoscele egale, apoi, pentru a găsi zona suprafeței laterale a piramidei, avem nevoie pentru a se multiplica aria unui triunghi isoscel (o suprafață laterală) 6: $ 120 de \ cdot 6 = $ 720