Luați în considerare ABC triunghiul $ $, în cazul în care $ _1, \ ~ 1 \ $ _1 mediana ei. Deoarece mediana este împărțit în două părți. Să considerăm midline $ A_1B_1 $ (Fig. 3).
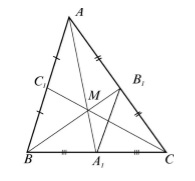
Figura 3. Ilustrarea Corolar 1
Prin Teorema 1, $ AB || A_1B_1 $ și $ AB = 2A_1B_1 $, prin urmare, $ \ unghi ABB_1 = \ unghiul BB_1A_1, \ \ unghiul BAA_1 = \ unghiul AA_1B_1 $. Deci, triunghiuri $ $ GBA și $ A_1B_1M $ similar cu prima baza similarității de triunghiuri. atunci
În mod similar dovedi că
Corolar 2: trei linia de mijloc a triunghiului se împarte în 4 triunghiuri similare cu originalul triunghi similaritate coeficient $ k = \ frac $.
Luați în considerare triunghiul $ ABC $ cu liniile centrale $ A_1B_1, \ _1C_1, \ B_1C_1 $ (fig. 4)
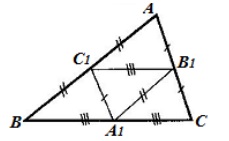
Figura 4. Ilustrarea Corolarul 2
Luați în considerare un triunghi $ A_1B_1C $. Deoarece $ A_1B_1 $ - linia medie,
Unghi $ C $ - unghi total al acestor triunghiuri. În consecință, triunghiuri $ A_1B_1C $ și $ ABC $ similară în a doua caracteristică triunghiuri similare cu coeficientul de similaritate $ k = \ frac $.
În mod similar, putem dovedi că triunghiuri $ A_1C_1B $ și $ ABC $, și triunghiuri $ C_1B_1A $ și $ ABC $ sunt similare cu coeficient de similaritate $ k = \ frac $.
Luați în considerare un triunghi $ A_1B_1C_1 $. De la $ A_1B_1, \ _1C_1, \ B_1C_1 $ - linia medie de triunghiul,
Prin urmare, conform unui al treilea aspect al similarității triunghiuri, triunghiuri $ A_1B_1C_1 $ și $ ABC $ similară cu similaritate coeficient $ k = \ frac $.
Exemple de obiective pentru conceptul de linia de mijloc a triunghiului
Dan triunghi cu laturile $ 16 $ cm, de 10 cm $ $ și $ 14 $ cm. Găsiți perimetrul unui triunghi ale cărui vârfuri se află în mijlocul laturilor triunghiului.
Deoarece vârfurile triunghiului sunt dorite în mijlocul laturile acestui triunghi, mâna - liniile mediane ale triunghiului original. Prin Corolarul 2, constatăm că partea dorită a triunghiului sunt egale cu $ 8 $ cm $ 5 $ cm $ 7 $ cm.
Dan triunghi $ ABC $. Punct de $ N \ și \ M $ - $ ale BC puncte de mijloc și $ AB $, respectiv (Figura 5.).
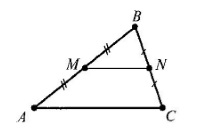
Perimetrul triunghiului $ BMN = 14 $ cm. Gasiti perimetrul triunghiului este ABC $ $.
Deoarece $ n \ i \ M $ - $ BC punctele de centru $ și $ AB $, atunci $ MN $ - linia medie. așa
Prin Teorema 1, $ AC = 2MN $. obținem: