Densitatea de probabilitate este definită aproape peste tot. În cazul în care o densitate de probabilitate și aproape peste tot în ceea ce privește Lebesgue măsură, și funcționează ca o densitate de probabilitate.
Integrala densității asupra întregului spațiu este egal cu unu:
.
Pe de altă parte, în cazul în care - non-negativ aproape peste tot funcția astfel încât să existe o măsură de probabilitate absolut continuă pe o astfel încât este densitatea acestuia.
Măsuri de înlocuire Lebesgue integrală:
,
în cazul în care orice funcție boreliană integrabilă în raport cu măsura de probabilitate.
Dispersie, tipuri și proprietăți ale dispersiei conceptului de dispersie
Variația în statisticile este abaterea medie pătratică a valorilor caracteristice individuale în pătratul mediei aritmetice. În funcție de datele inițiale se determină prin formule simple și varianțele ponderate:
1. Dispersie simplă (pentru date degrupate) calculat cu formula:
2. Varianța ponderată (pentru un număr de variante):
unde n - frecvența (repetabilitate factor X)
constatare de dispersie EXEMPLU
Pe aceasta pagina descrie exemplul standard, de a găsi dispersiei, puteți vedea, de asemenea, alte sarcini privind constatarea
Exemplul 1. Determinarea unui grup, media grupului și dispersia totală intergrup
Exemplul 2. Determinarea dispersiei și coeficientul de variație într-un tabel de grupare
Exemplul 3. Determinarea dispersiei într-un număr discret
Exemplul 4. Următoarele date sunt disponibile pentru un grup de 20 de studenți ai departamentului de corespondență. Avem nevoie de a construi un număr de distribuție interval caracteristic, se calculează valoarea medie a semnului și să examineze dispersia acestuia
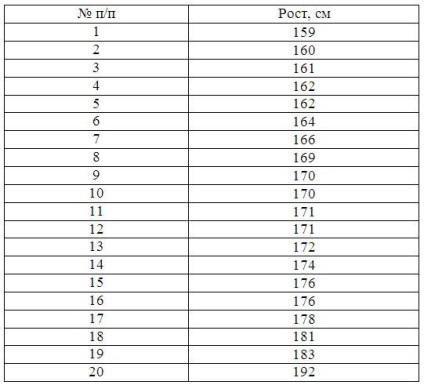
Noi construim grupul interval. Definim gama leagăn cu formula:
în care X caracteristică maximă grupare Max; X min minimă valoare caracteristică de grupare; n - numărul de intervale:
Acceptăm n = 5. Etapa egală cu: h = (192-159) / 5 = 6,6
Formează grupul interval
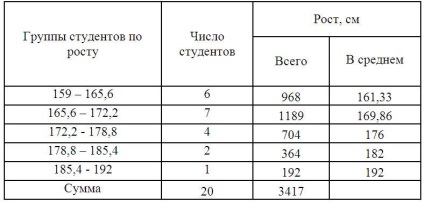
Pentru calcule vom construi tabel auxiliar:
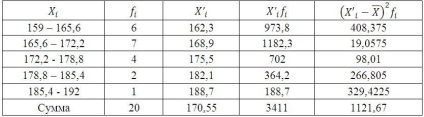
X'i- de mijloc a intervalului. (Pentru mid-range exemplu 159-165.6 = 162,3)
Valoarea medie a creșterii elevilor prin formula medie ponderată aritmetică:
Definim dispersia conform formulei:
Formula poate fi transformată după cum urmează:
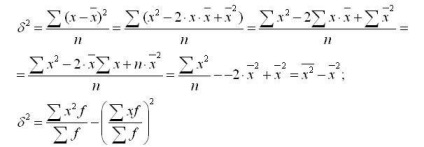
Din această formulă rezultă că mediul de dispersie este egală cu diferența dintre pătrate și o variantă pătrată și medie.
Dispersia în rânduri variaționale la intervale egale, în funcție de metoda momentelor următoare metodă poate fi calculată cu ajutorul a doua proprietăți de dispersie (divid toate variațiile asupra mărimii intervalului). Determinarea varianța. calculat prin metoda momentelor, cu următoarea formulă mai puțin laborioasă:
unde i - valoarea intervalului; A - zero, nominal este utilizat în mod convenabil interval de mijloc care are cea mai mare frecvență; m1 - puncte pătrate în primul ordin; m2 - momentul de ordinul doi
Dispersarea semn alternativ (dacă semn populația statistică este modificată, astfel încât există doar două realizări se exclud reciproc, o astfel de variabilitate numita alternativă) poate fi calculat prin formula:
Înlocuind în această formulă de dispersie q = 1- p, obținem:
tipuri de dispersie
Variația totală măsoară caracteristica de variație a întregii populații în ansamblul ei sub influența tuturor factorilor responsabili de această variație. Este egal cu media deviațiilor pătrate ale valorilor individuale ale caracteristice x valoarea medie totală de x și poate fi determinată ca o dispersie simplă sau ponderată varianță.
Intra-grup varianței caracterizează variația aleatorie, și anume, a variației, care este cauzată de influența factorilor neînregistrați și nu depinde de factorul caracteristic, situată în baza de grupare. O astfel de variație este valorile medii de eroare pătrat separa caracteristică în cadrul grupului X din media aritmetică a grupului și poate fi calculat la fel de simplu ca o variație ponderată sau dispersie.
Astfel, în cadrul aceleiași măsuri de dispersie caracteristice variației în cadrul grupului și este dată de:
unde xi - media grupului; Ni - numărul de unități din grup.
De exemplu, variația în cadrul grupului, care ar trebui să fie definit în sarcina de a studia impactul competențelor lucrătorilor la nivelul productivității muncii în magazin arată variații de ieșire din fiecare grup, cauzate de toți factorii posibili (starea tehnică a echipamentelor, furnizarea de instrumente și materiale, vârsta muncitorilor, intensitatea muncii, etc. .) cu excepția diferențelor de descărcare de calificare (în cadrul grupului de toți lucrătorii au aceleași calificări).
Medie de variație intra-grup reflectă variația aleatorie, T. E. Tu parte a variației care a avut loc sub influența altor factori, cu excepția factorului de grup. Se calculează după cum urmează:
dispersia Intergroup caracterizează variația variabilă rezultantă sistematică care este cauzată de influența factorului caracteristică, situată în baza de grupare. Este egal cu abaterea medie pătratică a mediilor de grup ale mediei globale. Între grupuri variance se calculează după cum urmează: