În rezolvarea problemelor aritmetice si algebrice este uneori necesară pentru a construi o fracție în pătrat. Cel mai simplu mod de a face acest lucru atunci când o fracție zecimală - doar un calculator obișnuit. Cu toate acestea, în cazul în care fracțiunea obișnuită sau mixtă, unele dificultăți pot apărea în timpul construcției acestor numere într-un pătrat.
- Calculator, calculator, aplicații Excel.
Pentru a construi o fracție zecimală în pătrat. Ia un calculator științific, introduceți-l ridicat în kvadratdrob și apăsați construcția celui de al doilea grad. Acest buton este pe cele mai multe calculatoare desemnate ca „h²“. În standard, funcția de calculator pentru Windows cvadratura se pare ca «x ^ 2" . De exemplu, pătratul zecimal este egal cu 3.14: 3,14² = 9,8596.
Pentru a pătrat zecimal pe un (contabilitate) Calculator normale, înmulțiți acest număr de la sine. Apropo, în unele modele de calculatoare cu condiția posibilitatea unui număr ridicat la pătrat, chiar și în absența unui buton dedicat. Prin urmare, pre-citit instrucțiuni la calculator special. Uneori, exemple de exponentiere „viclenie“, se arată în capacul din spate sau pe cutia calculatorului. De exemplu, pe mai multe calculatoare pentru construirea de pătrat, trebuie doar să apăsați butonul „x“ și „=“.
Pentru cvadratura fracțiune comună (constând din numărătorul și numitorul), ridicat la pătrat individual numărătorul și numitorul fracției. Aceasta este, utilizați următoarea regulă: (c / o) ² = ch² / z² unde h - numărătorului, s - numitor drobi.Primer: (3/4) ² = 3² / 4² = 9/16.
Dacă sunt construite în interiorul kvadratdrob - mixt (compus dintr-o parte întreagă și o fracție comună), pre-l aduce la mintea obișnuită. Aceasta este, se aplică următoarea formulă: (n c / o) ² = ((n * h + h) / h) ² = (s + n * h) ² / z² unde n - partea întreagă a drobi.Primer mixt: (3 2/5) ² = ((5 * 3 + 2) / 5) ² = (3 * 5 + 2) ² / 5² = 17² / 5² = 289/25 = 11 14/25.
Math Puzzle-urile sunt uneori transportate departe, astfel încât doresc să învețe cum să le creați, nu numai pentru a rezolva. Poate cel mai interesant pentru incepatori este de a oferi un pătrat magic care este un pătrat cu laturile de dimensiuni nxn pe care sunt înscrise numerele naturale de la 1 la n2 astfel încât suma numărului de linii orizontale, pătrat verticale și diagonale este aceeași și este egală cu un număr.

Înainte de a face pătrat dvs., să înțeleagă că ordinul a doua patrate magice nu se întâmplă. De ordinul al treilea pătrat magie există de fapt, doar unul, celălalt derivat din acesta sunt obținute prin rotație sau reflexie a axei principale de simetrie a unui pătrat. Cu cât este mai ordine, cu atât mai mult există posibile pătrate magice de ordine.
Aflați elementele de bază ale construcției. Reguli pentru construirea diferitelor pătrate magice sunt împărțite în trei grupe, în funcție de ordinea de pătrat, și anume acesta poate fi ciudat, egală cu de două ori sau de patru ori numărul impar. Metoda generală pentru construirea tuturor pătratelor nu există în prezent, deși foarte diferite scheme.
Utilizați un program de calculator. Descărcați aplicația dorită și valoarea dorită a pătratului (2-3), programul generează combinația digitală dorită.
Construieste-ti propriul pătrat. Ia matricea n x n. în interiorul căreia face construcția rombul în trepte. În ea umple toate patratelele de pe stânga și în sus pe toate diagonalele o secvență de numere impare.
Se determină valoarea celulei central A. La colțurile pătratului magic o astfel de poziție: celula din dreapta sus - O-1, stânga jos - D + 1, chiar în partea de jos - O-n, iar partea stângă - sus O + n. Celulele goale în unghiurile triunghiurilor umple, folosind regula destul de simplu: în rânduri de la stânga la dreapta pentru a mări numărul n + 1, și în barele în direcția de sus în jos pentru a crește numărul de n-1.
Descoperiți toate pătratele cu ordinul egal cu n este posibilă numai pentru n \ le 4, proceduri atât de interesante separate pentru construirea pătrate magice cu n> 4. Cel mai simplu mod de a calcula proiectarea pătrat de ordine ciudat. Profitați de o formulă specială, în cazul în care doriți să puneți doar datele necesare pentru a obține rezultatul dorit.
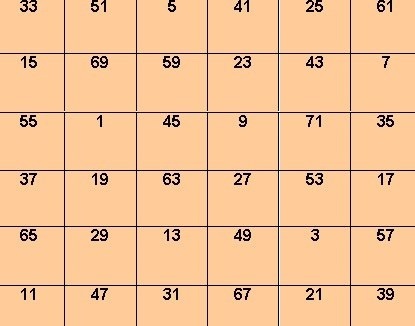
De exemplu, un pătrat constant, construit în cadrul schemei cu orez. 1 se calculează cu formula:
S = 6a1 + 105b,
în cazul în care A1 - primul membru al progresiei,
b - progresia diferența.