Conjunctia sau multiplicare logică (în teoria mulțimilor - această intersecție)
Conjunctie este o expresie logică complexă, care este adevărată dacă și numai dacă ambele expresii simple sunt adevărate. O astfel de situație este posibilă numai într-un singur caz, în toate celelalte cazuri, conjuncția este falsă.
denumire: , $ \ Wedge $, $ \ cdot $.
Tabelul de adevăr pentru conjuncțiilor

- În cazul în care cel puțin unul dintre sub-expresii ale conjuncției este fals pe un set de variabile, întreaga conjuncția este falsă pentru acest set de valori.
- Dacă toate expresiile conjuncției sunt adevărate la un anumit set de variabile, întreaga conjuncția este de asemenea adevărat.
- Semnificație întreaga conjuncție expresie complexă nu depinde de ordinul subexpressions înregistrare la care este aplicat (ca în multiplicarea matematică).
Disjuncție sau adăugarea logică (în teoria mulțimilor este o asociație)
Disjuncția este o expresie logică complexă, care este aproape întotdeauna adevărat, cu excepția cazului când toate expresiile sunt false.
Tabelul de adevăr pentru disjuncției

- În cazul în care cel puțin unul dintre sub-expresii ale disjuncției este adevărat pentru un anumit set de variabile, atunci întreaga disjungerea ia valoarea reală pentru un anumit set de sub-expresii.
- Dacă toate expresiile dintr-o listă de disjuncție false pe un set de variabile, atunci întreaga disjungerea acestor expresii, de asemenea, este falsă.
- Înțeles toate disjunctii nu sunt independente de subexpressions ordinea de intrare (la fel ca în matematică - plus).
Negație, negație sau inversiune (în teoria mulțimilor este o negație)
Negație - înseamnă că la expresia logică inițială se adaugă la particulele nu sau cuvinte nu este adevărat că, în cele din urmă vom găsi că, dacă expresia inițială este adevărată, negarea a originalului - este fals, și invers, în cazul în care expresia inițială este falsă, negația este adevărată.
Legenda: nu $ A $, $ \ bar $, $ ¬A $.
Tabelul de adevăr pentru inversiune
„Negativ dublu» $ $ ¬¬A este rezultatul judecății $ A $, adică tautologie are loc în logica formală și este egală cu valoarea în logica booleană.
Implicația sau consecință logică
Implicația - o expresie booleană complexă, care este valabil în toate cazurile, cu excepția de adevăr trebuie să mintă. Adică, această operație logică leagă două expresii simple, logice, dintre care prima este o condiție ($ A $), iar al doilea ($ A $) este o consecință a ($ A $).
Notația: $ \ la $, $ \ rightarrow $.
Tabelul de adevăr pentru implicație
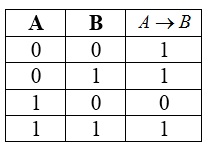
- $ A \ A la B = ¬A \ Vee B $.
- Implicația $ A \ A la B $ este falsă, dacă $ A = 1 $ și $ B = 0 $.
- Dacă $ A = $ 0, atunci implicația $ A \ A la B $ true pentru orice valoare de $ B $, (de minciună poate urmări adevărate).
Echivalare sau echivalență logică
Echivalența - este o expresie booleană complexă care este fidel valorile variabilelor egale cu $ A $ și $ B $.
Notația: $ \ $ leftrightarrow, $ \ Leftrightarrow $, $ \ $ echiv.
Tabelul de adevăr pentru echivalarea
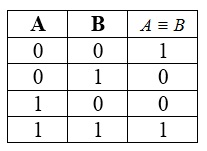
- Echivalența este adevărat în seturi egale de variabile $ A $ și $ B $.
- CNF $ A \ echiv B = (\ bar B \ vee) \ cdot (A \ cdot \ bar) $
- DNF $ A \ B = echivalent \ bar \ cdot \ bar \ vee A \ B $ cdot
disjuncție stricte sau modulo-2 (în teoria seturi este unirea a două seturi, fără a trece-le)
Strict disjuncție este adevărat în cazul în care argumentele nu sunt egale.
Pentru funcția de trei variabile și mai mult rezultatul operației este valabil numai atunci când numărul de argumente este egal cu $ 1 $, setul curent de componente - este ciudat. Această operație are loc în mod natural într-un inel modulo rest 2, de unde și numele operațiunii.
Atestari: $ A \ oplus B $ (în limbaje de programare), $ A ≠ B $, $ A $ B \ pană (în limbaje de programare).
Tabelul de adevăr pentru operația de adăugare modulo doi
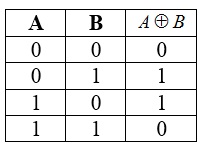
Proprietăți disjuncție stricte:
- $ A \ oplus 0 = a $ (idempotența)
- $ A \ oplus 1 = \ bar $ (negație)
- $ A \ oplus a = 0 $ (primirea 0)
- $ A \ oplus b = b \ oplus un $ (comutativ)
- $ (A \ oplus b) \ oplus c = a \ oplus (b \ oplus c) $ (asociativitatea)
- $ (A \ oplus b) \ oplus b = a $ (absorbție)
- $ \ Bar \ oplus b = o \ oplus \ bar = (a \ echiv b) $ (congruenta modulo)
Pierce săgeată
Operația logica binară, o funcție booleană de două variabile. Numit în onoarea lui Charles Pierce și introdus în algebra logicii în $ $ 1880-1881 gg.
Notația: $ \ downarrow $. NOR
Tabelul de adevăr pentru logică și nici
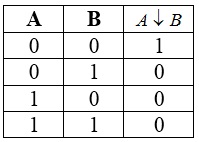
Logic și nici ca conjuncție, disjuncție, negație, formează o bază pentru funcțiile booleene a două variabile. Cu ajutorul logic și nici nu se poate construi toate celelalte operații logice, cum ar fi:
$ X \ downarrow X = ¬X $ - negare
$ (X \ downarrow Y) \ downarrow (X \ downarrow Y) \ echiv X \ vee Y $ - disjuncție
$ (X \ downarrow X) \ downarrow (Y \ downarrow Y) \ echiv X \ pană Y $ - conjuncție
$ ((X \ downarrow X) \ downarrow Y) \ downarrow ((X \ downarrow X) \ downarrow Y) = X \ Y $ - implicare
În electronică, logice și nici reprezentate sub forma unui element, care se numește "operațiune 2or-NO" (NOR-2-in).
accident vascular cerebral Sheffer
Funcția booleană a două variabile sau logice binare. Introducem Genri Shefferom în 1913
Atestari: $ | $, este echivalent cu operația AND-NOT.
Tabelul de adevăr pentru funcția Sheffer accident vascular cerebral

Sheffer accident vascular cerebral formează baza pentru toate funcțiile booleene a două variabile. Aplicarea accident vascular cerebral Sheffer poate construi restul operațiunii, de exemplu,
$ X \ mijlocul lui X = ¬X $ - negare
$ (X \ mid Y) \ mid (X \ mid Y) = (X \ Y pană) $ - conjuncție
$ (X \ la mijlocul X) \ la mijlocul (Y \ Y mijlocul anului) = X \ vee Y $ - disjuncție
$ X \ la mijlocul ¬X $ - constanta 1
Pentru electronică, acest lucru înseamnă că schemele de implementare posibile cu ajutorul unui element de model (deși acest lucru este un element scump).
Ordinea executării operațiilor logice într-o expresie logică complexă
- Inversion (negație);
- Conjuncția (multiplicare logică);
- Disjuncție și disjuncție strict (plus Boolean);
- Implicația (consecință);
- Echivalența (identitate).
Rezolvarea controlului în toate subiectele. 10 ani de experiență! Preț de la 100 de ruble. Perioada de la 1 zi!