Pagina 3 din 4
Acum, după ce să se familiarizeze cu statistici ca o modalitate de a descrie datele, suntem gata să apeleze la interpretarea datelor - cum să tragă concluzii din ele.
În primul rând, este necesar să se facă distincția între un grup și un eșantion de grup. Statele Unite ale Americii Census Bureau încearcă să descrie populația în ansamblu, prin obținerea materialului descriptiv privind vârsta, starea civilă și așa mai departe. D. Toți locuitorii țării. Potrivit grupului (populație) este potrivit pentru Census Bureau, deoarece reprezintă toți oamenii care trăiesc în Statele Unite.
În statisticile, „gruparea“ cuvânt nu este limitat la oameni, animale sau obiecte. Grupul poate fi valoarea tuturor temperaturilor, termometrul înregistrat în ultimul deceniu, toate cuvintele din limba engleză, sau orice alt stoc de date specifice. De multe ori nu avem acces la întregul grup, iar apoi vom încerca să-l prezinte în proba prelevată la întâmplare
Procedura (nepărtinitoare). Puteți pune orice întrebare a unei părți selectate aleatoriu din oameni, așa cum a făcut-Census Bureau într-un recensământ recent; Puteți obține temperatura medie, de a scoate termometrul la un anumit timp și nu efectuează o înregistrare continuă; putem estima numărul de cuvinte în enciclopedie, numărând cuvintele dintr-un pagini selectate aleatoriu. In toate aceste exemple este o probă din grup. Dacă oricare dintre aceste procese se repetă, rezultatele sunt puțin diferite datorită faptului că eșantionul nu reflectă pe deplin grupul ca întreg și, prin urmare, cuprinde eroarea de eșantionare. Este aici că vin în inferență statistică joc.
Exemplu de date colectate de grup pentru a face o concluzie cu privire la acest grup. Puteți examina un eșantion de date de recensământ pentru a afla dacă îmbătrânirea populației, de exemplu, și dacă există o tendință de migrație în zonele suburbane. În mod similar, rezultatele experimentale sunt studiate pentru a determina ce impact a avut manipulările experimentale asupra comportamentului - în cazul în care volumul pe pragul de percepție a pasului afectat, sau dacă educația au un impact deosebit de semnificativ asupra vieții viitoare. Pentru a face deducții statistice, este necesar să se evalueze relația, moment în care datele eșantion. Aceste concluzii sunt întotdeauna un anumit grad de incertitudine din cauza unei erori de eșantionare. În cazul în care testele statistice indică faptul că amploarea efectului, se găsește în eșantion este suficient de ridicată (evaluarea relativă a erorii de eșantionare), atunci putem fi siguri că există efectul observat în eșantion din grupul ca întreg.
Astfel, inferență statistică este necesitatea de a trage o concluzie sau hotărâre cu privire la anumite grupuri caracteristice bazate numai pe informațiile obținute cu privire la eșantion din acest grup. În ceea ce datarea concluzia statistică considerăm distribuția normală și utilizarea sa în interpretarea abaterii standard.
Atunci când o cantitate mare de date colectate, sunt tabelate și afișate în formă histogramă sau plic, ele formează adesea o distribuție simetrică în formă de clopot, cunoscut sub numele de distribuția normală. Cele mai multe dintre componentele sale sunt situate în apropierea (punctul de clopot de sus) de mijloc, iar clopotul scade brusc la cea mai mare și cea mai mică valoare. O astfel de formă a curbei prezintă un interes deosebit, deoarece apare chiar și atunci când rezultatul procesului bazat pe setul de evenimente aleatorii, toate care au loc în mod independent. Dispozitiv de demonstrație așa cum este prezentat în Fig. P4, vă permite să vedeți evenimente cum aleatoare de distribuție normală pliat. factor aleator - dacă bila de oțel toamna la stânga sau la dreapta de fiecare dată când ajunge la furca - conduce la distribuirea simetrică: mai multe bile sunt în scădere chiar în mijloc, dar din când în când unul ajunge la unul dintre birourile exterioare. Aceasta este o vizualizare la îndemână a ceea ce se înțelege printr-o distribuție aleatorie apropiată de distribuția normală.

Fig. P4. Un aparat pentru a demonstra o distribuție variabilă aleatoare normală.
Aparatură a avut loc cu susul în jos, până când toate bilele de oțel nu se rostogolească în jos, în rezervor. atunci
dispozitivul este răsturnat și se păstrează pe verticală până când granulele trec prin câmp cu știfturile, nu să se scufunde în adânciturile 9 în partea de jos a coloanelor. Numărul exact de bile capturate în fiecare coloană, în diferite demonstrații vor varia. Cu toate acestea, înălțimea medie a coloanelor de bile se va repeta de distribuție aproximativ normală atunci când cea mai mare coloana va fi în centru, iar înălțimea celorlalte difuzoare vor fi reduse spre margini.
Distribuția normală (Figura P5.) - este o reprezentare matematică a distribuției idealizată a generat aproximativ dispozitivul prezentat în Fig. P4. Distribuția normală indică probabilitatea ca elementele din grupul cu distribuție normală va fi diferită de media la orice valoare dorită. Procentul din Fig. P5 este o fracțiune din aria de sub curba situată între valorile scalei menționate anterior; suprafața totală de sub curba corespunde grupului ca întreg. Aproximativ două treimi din totalul cazurilor (68%) se încadrează în intervalul între plus și minus o deviație standard de la medie (± 1g); 95% din cazuri - în intervalul ± 2G; și, practic, toate cazurile (99,7%) - la ± 3G.
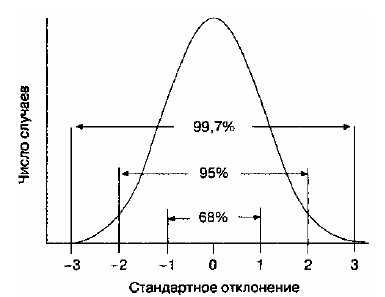
Fig. P5. Distribuția normală. puteți construi o curbă de distribuție normală, folosind deviația standard și medie. Aria de sub curba care se află la stânga și la dreapta + 3a-3a poate fi neglijată.
O listă mai detaliată a suprafețelor pieselor curbe normale indicate în tabelul. P4.
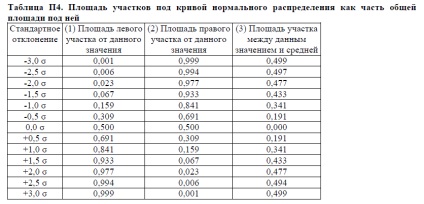
Să folosim masa. urme P4 ca valori derivate de 68% și 95%, prezentat în Fig. P5. Tabel. P4 în coloana a treia, constatăm că între -1g și media este de 0.341, iar suprafața totală cuprinsă între + 1 ° și medie prea 0.341 suprafața totală. In concluzie, aceste valori dau 0,682 ca în Fig. P5 este prezentat ca 68%. In mod similar zona de la -2o la + 2o este de 2 x 0,477 = 0,954, prezentat ca 95%.
Pentru a interpreta figura, de multe ori trebuie să știe, este mare sau mic în raport cu alți indicatori. În cazul în care o persoană care oferă testul de conducere este necesară 0.500 secunde pentru a apăsa pe frână după semnalul de urgență, cum să-l identifice rapid sau lent? Credeți că un student a trecut un curs în fizică, în cazul în care înregistrarea lui în examen este de 60? este necesar să se aducă scara cu care acești parametri pentru a răspunde la astfel de întrebări pot fi comparate.
rang de date. Cu cifre în rang de la mare la mic, vom obține unul dintre aceste scale. Un indicator separat este interpretat de faptul în ce moment el este printre un grup de indicatori. De exemplu, studenții Academiei Militare West Point știe unde se află în clasa - probabil 35-biți sau 125-mi într-o clasă de 400.
Rata standard. Deviația standard - o unitate de scalare convenabil, așa cum putem aprecia cât de departe de media sunt situate 1 ° sau 2 ° (tabelul A4.). Valoarea produsului, în care un factor - deviația standard, numit o masura standard. Multe scale utilizate în măsurători psihologice, bazate pe principiul unui indice standard.
Exemplu de calcul al indicelui standardului. Tabel. P1 prezintă cifrele obținute de 15 elevi din examenele de admitere. Fără a avea mai multe informații, nu știm dacă aceste cifre sunt reprezentative pentru grupul tuturor solicitanților. Cu toate acestea, să presupunem că mediana în aceste examene a fost de 75, și o deviație standard de 10.
Care va fi măsura standard a unui student, care a marcat 90 de puncte la examene? Cum este peste medie această cifră trebuie să fie exprimate în numărul de deviații standard:

În acest caz, componenta de student se află sub media de 2,2 deviații standard. Astfel, semnul valorii standard, (+ sau -) indică faptul că, deasupra sau dedesubtul indicatorului mediu este activ și valoarea sa indică cât de departe este de la medie în unități de deviație standard.
Cum medie reprezentativ?
Cât de bine eșantionul mediu reflectă media întregului grup? Dacă măsurăm creșterea într-un eșantion aleatoriu de 100 de studenti de colegiu, cât de bine media eșantionului prezice adevărata medie a grupului (de exemplu, creșterea medie a tuturor elevilor de colegiu)? Acestea sunt toate problemele legate de încheierea grupului, pe baza datelor de eșantionare.
Precizia acestei concluzii depinde de eroarea de eșantionare. Să presupunem că am făcut două eșantioane aleatorii din același grup și pentru fiecare dintre ele se calculează media. Care este diferența între unul și celălalt mediu poate fi de așteptat, ca urmare a cazului?
eșantioane aleatorii ulterioare din același grup va oferi suport diferit, formând o distribuție de medie probă în jurul adevăratul media grupului. Aceste medii de probă propriu-zise sunt valorile pentru care este posibil să se calculeze deviația standard. Aceasta este o deviație standard numită eroare standard a mediei; acesta este notat sM și calculată folosind următoarea formulă:
în cazul în care o - abaterea standard a eșantionului și N - numărul de cazuri pentru care media se calculează pentru fiecare.
Conform acestei formule, eroarea standard valoarea medie scade odată cu creșterea dimensiunii eșantionului; astfel încât media, bazată pe un eșantion mai mare este mai de încredere (probabil va fi mai aproape de adevărata medie a întregului grup). Acest lucru a fost de așteptat să fie pe baza de bun simț. SEM arată în mod clar modul în care incert media obținută. Cu cât mărimea eșantionului, cea mai mică incertitudinea medie.
In multe experimente psihologice, datele sunt colectate pe două grupe de subiecți; un grup este expus la un anumit efecte experimentale, iar celălalt servește ca un control. Problema este dacă există o diferență între mediile acestor grupuri, și dacă este așa, dacă se menține pentru întregul grup, din care au fost luate aceste două mostre. Pur și simplu pune, în cazul în care diferența dintre cele două grupuri reflectă o adevărată diferență sau a apărut din cauza unei erori de eșantionare.
Ca un exemplu, compara testul de performanță de citire la rate de eșantionare malchikov- clasa intai cu clasa intai din eșantion-and-fete. În ceea ce privește media, acestea sunt mai mici decât la băieți, dar există o suprapunere considerabilă; unii băieți face excepțional de bine, iar unele dintre fete - foarte proaste. Prin urmare, nu putem accepta acest mediu diferență, fără a efectua un test de semnificație statistică. Numai atunci putem decide dacă reflecta diferențele observate în eșantion diferențele reale din grup sau în care sunt explicate prin eroarea de eșantionare. Dacă unele dintre fete mai talentați și unii dintre băieți mai stupide au fost alese întâmplător, diferența poate fi explicată prin eroarea de eșantionare.
Ca un alt exemplu, să presupunem că am efectuat un experiment decât o strângere de mână pentru bărbați cetății righties și lefties. În partea superioară a tabelului. P5 arată datele ipotetice ale acestui experiment. O probă de 5-handers bărbați cu o medie de probă de 8 kg mai puternic de 5 bărbați handers. Ceea ce, în general, pot fi deduse din aceste date despre bărbați și righties stângaci? Putem spune că Dreptaci este mai puternic? Evident că nu, din moment ce media obținută în majoritatea dreptaci, nu ar fi diferită de media în majoritatea stângaci; Un demn de remarcat oferind valoare de indicator de 100 indică faptul că avem de-a face cu o situație incertă.
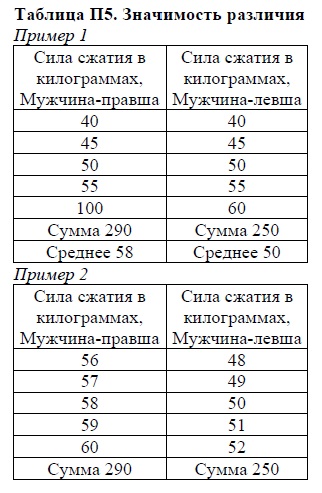
Acum, să presupunem că, ca urmare a rezultatelor experimentului obținute, se arată în partea de jos a aceluiași tabel. P5. Încă o dată vom vedea aceeași diferență între media de 8 kg, dar acum această informație este mai credibilă, deoarece indicii de oameni stângaci au dovedit a sistematic mai mică decât cea a dreptaci. Statisticile vă permite să luați cu precizie în considerare fiabilitatea diferențelor medii, astfel încât determinarea care dintre cele două diferențe este mai sigură, nu depinde numai de intuiție.
Aceste exemple arată că semnificația diferențelor obținute depinde de mărimea ei, iar variabilitatea mediilor comparate. Cunoscând eroarea standard a mediei, este posibil să se calculeze eroarea standard a diferenței dintre cele două mijloace odm. Apoi, diferența rezultată poate fi estimată folosind relația critică - o relație derivată diferență medie (DM) la eroarea standard a diferenței dintre media:
Acest lucru îi permite să evalueze semnificația diferențelor dintre cele două medii. Ca o regulă simplă, atitudinea critică ar trebui să nu fie mai mică de 2,0 la diferența medie a fost considerată semnificativă. De-a lungul acestei cărți, expresia „semnificație statistică“ înseamnă diferența înseamnă că critica dintre ei cel puțin asta.
De ce un raport critic selectat semnificative statistic egal 2.0? Doar pentru că o astfel de valoare mare sau poate cădea accidental doar 5% din cazuri. În cazul în care a făcut 5%? atitudine critică poate fi considerată ca o măsură standard pentru ca este doar o diferență de două medii, exprimate în numărul de erori standard. Referindu-se la a 2-a coloană a tabelului. P4, rețineți că probabilitatea ca abaterea standard este de 2,0, în caz de coincidență accidentală este egală cu 0,023. Deoarece probabilitatea de deviație în direcția opusă este de asemenea egală cu 0.023, probabilitatea generală este 0,046. Aceasta înseamnă că, atunci când media grupuri sunt identice, raportul critic poate fi accidental egal cu 2,0 (sau mai multe), în 46 de cazuri din 1000, sau 5% din cazuri.
Elementar în general, că raportul critic nu trebuie sa fie mai mic de 2,0, și anume astfel - este de regulă arbitrară, dar convenabil, care specifică nivelul de 5% din semnificație. Ca urmare a acestei reguli, probabilitatea unor decizii eronate care există diferența medie atunci când de fapt nu este, va fi mai mică de 5%. Nu neapărat să folosească un nivel de 5%; în unele experimente ar putea necesita o semnificație mai mare, în funcție de cât de mult de eroare este concluzia acceptabilă.
Exemplu de calcul al ratei critice. Pentru calcularea relațiilor critice necesare pentru a determina eroarea standard a diferenței dintre cele două medii, după cum urmează:
În această formulă, OM1 și OM2 - eroare standard a comparat două medii.
Ca o ilustrare, să presupunem că avem nevoie pentru a compara realizările clasa intai - băieți și fete în examenul din Statele Unite ale Americii citi. Ia-un eșantion aleatoriu de băieți și fete de testare. Să presupunem că media este de 70 de băieți cu o eroare standard a mediei 0.40 și mediane fete - 72 la eroarea standard a mediei de 0,30. Pe baza acestor probe trebuie să decidă dacă există o diferență reală între succesul băieților și fetelor în lectura în grup ca întreg, de eșantionare a datelor arată că estimările fetelor mai mult decât băieții, dar este posibil să se concluzioneze că vom obține același prin testarea tuturor SUA clasa intai? Rezolva permite atitudine critică.
Deoarece raportul critic semnificativ peste 2,0, se poate argumenta că diferența medie observată este statistic semnificativă la nivelul de 5%. Prin urmare, putem concluziona că există o diferență de încredere în lectură progres între băieți și fete. Rețineți că raportul critic poate fi pozitiv sau negativ, în funcție de ce fel de mediu a scăzut; la o interpretare critică atitudine ia în considerare doar amploarea, dar nu semnul.