În cazul în care fiecare punct din planul este atribuit un punct în același plan, și dacă în orice punct în acest plan este mapat la un anumit punct, atunci spunem că această cartografiere a planului pe sine. Orice cartografiere planul în care rămân la distanță constantă între punctele se numește planul de mișcare.
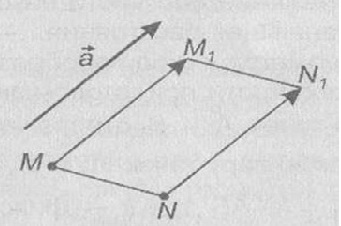
transfer paralel. Să o - acest vector. Traducere paralel de către un vector numit maparea a planului, în care este afișat fiecare punct M la punctul de M1. vector MM1 care este vectorul o.
transferul paralel al unei mișcări, așa cum este cartografierea planului pe care păstrează distanțe. Intuitiv, această mișcare poate fi reprezentat ca o schimbare a întregului plan în direcția vectorului și lungimea acestuia.
Turn. Denote punctul plan O (centru de rotație) și definește un unghi α (unghiul de rotație). Rotirea planului în jurul punctului O, cu un unghi α se numește cartografierea planului, în care este afișat fiecare punct M la punctul de M1. care OM = OM1 și unghiul MOM1 egal cu a. În acest caz, punctul O rămâne în locul său, care este afișat în sine pe, și toate celelalte puncte sunt rotite în jurul punctului O în aceeași direcție - .. sau în sens invers acelor de ceasornic (figura arată invers acelor de ceasornic rotație).
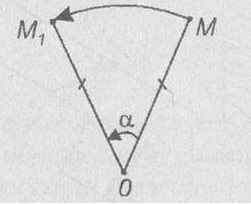
Rotația este o mișcare, așa cum este planul de afișare, în care distanțele memorate.
plan de transformare geometrică în care fiecare pereche de punctele A și B este afișat pe o pereche de puncte A1 și B1. că A1 B1 = k ∙ AB, unde k - fix pentru această conversie este o constantă pozitivă numită o transformare de similaritate. Numărul k este apelat cu coeficientul de similitudine.
Este evident faptul că planul de mișcare - caz similitudine privat (un factor de 1).
Figura F, numită astfel de cifră F. Dacă există o transformare similaritate în care o figură F este afișată în figura F1. Astfel, aceste cifre diferă numai în mărime, formă F și F1 forme identice.
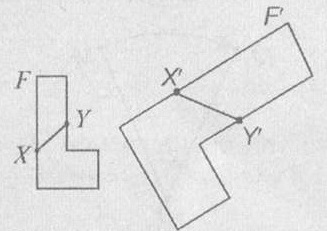
Proprietăți similitudine de transformare.
- Transformarea similaritate păstrează perechile segmente de relație: dacă AB și CD - două de lungime arbitrară și A1 și B1 C1 D1 - imaginile lor, A1 B1 / C1 D1 = AB / CD.
- segmente egale sunt afișate în egală; punctul de mijloc - în mijlocul imaginii sale.
- Dacă planul specificat două sisteme de coordonate rectangulare, și având numărul k> 0. transformarea similaritate apoi definită în mod unic cu un coeficient k care afișează axa sistemului de coordonate mai întâi în aceeași axă secundă.
plan de transformare geometrică, cu un punct fix S, care fiecare punct A, este diferit de S, atribuie un punct A1. că SA1 = k ∙ SA, unde k ≠ 0 - preasigurată număr, numit un homothety cu centru de S k și un coeficient. Dacă F1 cifră este derivată din figura F folosind dilatarea, cifra F și F1 sunt numite homothetic.
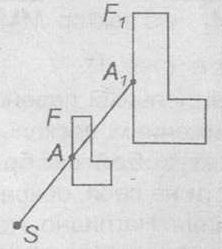
- Homothety cu coeficientul k este o similitudine cu factor de │k│.
- Dil ia orice linie dreaptă, în paralel cu linia ei.
- Orice homothety poate fi setat centrul homothetic și o pereche de puncte reciproc corespunzătoare.