
Nici un investitor sănătos nu ar investi în necunoscut. Este important să fie în măsură să evalueze riscurile și beneficiile potențiale de a investi. Aici sunt conceptele de bază necesare pentru o descriere cantitativă a procesului de investiții.
Interes, simplu și compus
Procentul - un venit sub formă de bani plătite pentru creditor pentru utilizarea banilor lui. Dobânda se calculează pe valoarea principală a depozitului (împrumut), la o rată a dobânzii la intervale regulate (de exemplu, anual sau trimestrial). Procentul poate fi simplu și complex.
Luați în considerare încorporarea de 1000 EUR pe un cont bancar pentru o perioadă de 5 ani, la o rată de 12% pe an. În cazul în care, după fiecare an, proprietarul elimină venitul plătit pe depozit, rezultatele de investiții sunt după cum urmează:
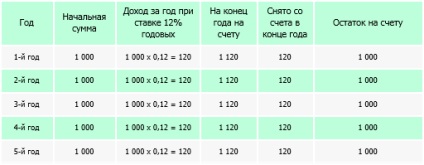
Ca urmare, de investiții sau de 5 ani a primit 5 x 120 = 600 EUR peste valoarea depozitului initial.
Astfel, valoarea totală a fondurilor la sfârșitul celui de al cincilea an va fi de 1600 de euro.
Aceasta este, dobânda simplă calculată pe baza ratei dobânzii și valoarea inițială, indiferent de dobânda acumulată. Această schemă corespunde cazului în care venitul din depozit este plătit periodic de către debitor și creditor imediat retras.
Luați în considerare încorporarea de 1000 EUR pe un depozit bancar pentru o perioadă de 5 ani de la aceeași rată de 12% pe an, dar cu condiția ca proprietarul nu elimină sfârșitul fiecărui an, veniturile, și le lasă într-un cont în scopul reinvestirii la aceeași rată (12 %):
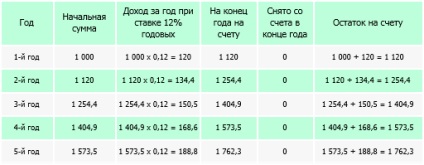
La sfârșitul celor cinci ani, investitorul va primi, în plus față de suma principală a contribuțiilor încă 762,3 EUR.
Valoarea totală a fondurilor la sfârșitul celui de al cincilea an va fi de 1 762,3 EUR.
Compusul de interes se calculează pe baza ratei dobânzii și suma acumulată în contul la începutul perioadei următoare, inclusiv veniturile acumulate. Această schemă corespunde cazului în care veniturile din depozit plătite de către împrumutat din când în când, dar nu au fost retrase creditor și debitor rămâne, crescând valoarea creditului.
Astfel, dacă vom compara condițiile fără a fi nevoie să investească veniturile acumulate (dobânzi simplă) și luând în considerare veniturile din investiții acumulate (dobânda compusă), rezultatul net pentru a doua schemă depășește rezultatele primei la 162,3 EUR. Acest lucru sa datorat reinvestirea continue a veniturilor primite. Creditorul în acest caz, este expus la un risc mai mare, respectiv, și primește o recompensă mai mare.
Modificarea valorii timp a banilor
Atunci când plasarea fondurilor disponibile în diverse valori mobiliare ale investitorului urmărește să obțină beneficii maxime. Presupunând că fiabilitatea absolută a tuturor moduri de a investi în scopul de a selecta modul optim de a investi, aveți nevoie pentru a compara veniturile. Cu toate acestea, venitul poate veni la momente diferite. Astfel, diferite moduri de plumb de investiții la diferite programe de a face bani.
In exemplul de mai sus №1 valoarea totală a fondurilor la sfârșitul celui de al cincilea an de investiții este de 1600 de euro. Această sumă se numește valoarea viitoare a banilor (1 000 de euro), care
- investit timp de 5 ani;
- la rata de 12% acumulate anual;
- fără reinvestirea (venituri de 12% este luată la sfârșitul fiecărui an).
La rândul său, investiția inițială în valoare de 1 000 EUR, menționată ca valoarea actuală a banilor (1 600 de euro), care
- Ele se obțin după 5 ani;
- la rata de 12%, evaluat pe an;
- fără reinvestirea (venituri de 12% este luată la sfârșitul fiecărui an).
Prin urmare, în exemplul №2 valoarea totală a fondurilor la sfârșitul celui de al cincilea an de investiții este de 1 762,3 EUR. Această sumă se numește valoarea viitoare a banilor (1 000 de euro), care
- investit timp de 5 ani;
- la rata de 12% acumulate anual;
- cu condiția reinvestit (creștere de 12% pe an nu este retras, și se adaugă la suma investiției inițiale).
La rândul său, investiția inițială în valoare de 1 000 EUR, menționată ca valoarea actuală a banilor (1 762,3 euro), care
- Ele se obțin după 5 ani;
- la rata de 12%, evaluat pe an;
- cu condiția reinvestit (creștere de 12% pe an nu este retras, și se adaugă la suma investiției inițiale).
Acum obținem formula pentru calcularea valorii viitoare a banilor investiți pentru o anumită perioadă sub un anumit procent, fără a reinvestirii și reinvestire:
Fara reinvestind, simpla formula interes №1:
Cu reinvestment, compus interes formula №2:
FV (Future Value) - valoarea viitoare a banilor;
PV (Present Value) - valoarea actuală (valoarea inițială la momentul investiției = valoarea principalului investiției inițiale);
r - rata dobânzii pe parcursul perioadei de calcul, exprimată ca fracție de unitate (în exemplele noastre, dacă rata este de 12%, valoarea r este 0,12);
n - numărul de perioade de compunere.
Acum este posibil să se înlocuiască valorile cunoscute în formulă, și mult mai rapid pentru a calcula valoarea viitoare din totalul fondurilor pentru două exemple noastre:
r = 0.12 (12%)
Exemplul №1 - fără a reinvesti interes, simplu:
FV = 1000 x (1 + 5 x 0.12) = 1600 EUR
Exemplul №2 - cu reinvestire interes compus:
FV = 1000 x (1 + 0,12) = 1 5 762,3 EUR
În cazul unei perioade (n = 1), ambele formule calculate din valori coincid complet, la fel ca în cazul unui interval de timp (în exemplele noastre este de 1 an) reinvestită în fapt are loc și condițiile de desen pentru simple și complexe obținute cu același procent.
mod natural de a compara fluxurile de numerar la momente diferite este de a le aduce la același punct în timp. Ca o regulă, cum ar fi timpul sau de pornire selectat de investiții sau un punct fix în viitor. În consecință, reducerea fluxurilor de numerar la un anumit punct, în viitor, este numit de incrementale, dar la momentul inițial - scontarea.
Calcularea valorii viitoare a banilor reinvesti folosind formula de interes compus numit de incremental (compunere). și expresia (1 + r) n se numește coeficientul de compoundare - ksFormula №3:
Calcularea inversa numit scontarea înregistrate în avans. La scontarea, putem afla cât de multe acum (în momentul de calcul) ar trebui să știe valoarea viitoare cu formula bani №4:
Inversul factorului de compoundare se numește factorul de actualizare - kdFormula №5:
Calcularea ratelor anuale ale dobânzilor
Expresia standard general acceptată a rentabilității investiției este considerată a se obține procente pe an. Uneori, cu toate acestea, rata dobânzii de rentabilitate pot fi specificate pentru diferite perioade de timp: în zile, săptămâni, luni, trimestre.
În acest caz, pentru a calcula dobânda anuală folosind formule speciale:
Dacă venitul este calculat prin simpla interes, investiția pe unitate a ratei anuale procentuale (rgodovaya), exprimată ca zecimală, se calculează după cum urmează: Formula №6:
r - rata exprimată ca zecimală;
n - numărul de perioade într-un an.
depozitele bancare La taxa trimestrial de 3% din suma depozitului initial fara reinvestire. Găsiți rata anuală de interes:
rgodovaya = r x n = 4 x 0,03 = 0,12 Sfertul An (12%)
La depozitele bancare plătesc lunar 1,5% din suma depozitului initial fara reinvestirea. Găsiți rata anuală de interes:
rgodovaya = r x n = 0,015 x 12 luni ale anului = 0,18 (18%)
Dacă venitul este calculat dobânda cumulată, investiția pe unitate a ratei anuale procentuale (rgodovaya), exprimată ca zecimală, se calculează după cum urmează: Formula №7:
r - rata exprimată ca zecimală;
n - numărul de perioade într-un an.
La depozitele bancare acumulați venituri trimestriale de 3% din valoarea inițială a contribuției din reinvestirea veniturilor primite. Găsiți rata anuală de interes:
rgodovaya = (1 + 0,03) 4 - 1 = 0.1255 (12,55% pe an)
La taxa de depozit bancar un venit lunar de 1,5% din suma inițială de depozit cu reinvestirea veniturilor primite. Găsiți rata anuală de interes:
rgodovaya = (1 + 0,015) 12-1 = 0.1956 (19,56% pe an)
Comparând rezultatele calculelor, puteți face încă o dată asigurați că rata anuală a dobânzii, ținând cont de reinvestire întotdeauna mai mare, ceteris paribus.
Dacă randamentul indicat în raport cu o perioadă de lucru (de exemplu, 0,1% pe zi, 0,5% pe săptămână, 1,5% pe lună sau pe trimestru 3%), dificultățile speciale cu calcularea ratei anuale a dobânzii nu apar.
Uneori, cu toate acestea, randamentele pot fi indicate în raport cu perioada de non-standard, de exemplu, „contribuția la banca dă 1,5% în 20 de zile.“ În acest caz, procesul de calcul al ratei anuale procentuale este puțin mai complicat, iar primul lucru pe care vom avea nevoie pentru a calcula valoarea în n (număr de perioade într-un an):
În cazul în care perioada de investiții este exprimat în zile. numărul de perioade într-un an:
X- în cazul în care numărul de zile.
În cazul în care perioada de investiții este exprimat în săptămâni. numărul de perioade într-un an:
în cazul în care X numărul de săptămâni.
În cazul în care perioada de investiții este exprimat în luni. numărul de perioade într-un an:
în cazul în care X numărul de luni.
În cazul în care perioada de investiții este exprimat în sferturi. numărul de perioade într-un an:
X- în cazul în care numărul de blocuri.
Banca Contribuția dă 1,5% în 20 de zile.
Găsiți rata anuală a dobânzii (simplu, fără reinvestire).
În primul rând vom calcula valoarea lui n:
n = 365/20 = 18,25
Adică, într-un an vom obține 18.25 „perioadă de 20 de zile.“
Acum este posibil să se calculeze rata anuală a dobânzii la Formula №6:
rgodovaya = 0,015x18,25 = 0,2738 (27,38% apr)
Banca Contribuția dă 4% la 1,5 luni. Găsiți rata anuală a dobânzii (combinat cu reinvestire).
În primul rând vom calcula valoarea lui n:
Adică, într-un an vom obține 8 „perioadă de jumătate de lună.“
Acum este posibil să se calculeze rata anuală a dobânzii la Formula №7:
rgodovaya = (1 + 0,04) la 8 - 1 = 0,685 (36,85% pe an)
Aducerea ratelor dobânzilor la o singură perioadă de timp
Este evident că, în aceleași condiții (același timp, simplu sau un interes compus) este mai profitabil că investițiile are o rată a dobânzii mai mare. Dar, de multe ori termenii perioadelor de investiții și de plată nu sunt aceleași pentru el. În acest caz, pentru a compara diferitele investiții, este necesar să se calculeze ratele dobânzii reduse la una și aceeași perioadă de timp. De regulă, anul ales ca această perioadă.
Compara care a depozitelor bancare este mai profitabil (în procente pe an):
Contributia №1 sub 1,5% pe lună; sau
№2 contribuție cu 10% în șase luni.
Calculul ratelor anualizate poate fi realizată în conformitate cu formula de procente simple sau complexe.
Calculăm prima formulă de interes simplu:
Calculați ce venitul ca procent din luna în al doilea caz, și compară cu deja de indicatorul în primul caz: o cotă de 10% din numărul de luni în această perioadă (șase luni):
Acum vom calcula rata la suta pe an pentru ambele cazuri prin Formula №6:
Contributia №1: rgodovaya = 0,015x12 = 0,18 (18%).
Contributia №2: rgodovaya = 0,0167x12 = 0,20 (20% pa).
Astfel, în cazul în care venitul este calculat conform formulei de interes simplu, contribuția №2, exprimată ca procent pe an, contribuția benefică №1.
Dacă venitul este calculat conform formulei dobânzii compuse, rata la suta pe an calculat cu formula №7:
Contributia №1: rgodovaya = (1 + 0,015) 12-1 = 0.1956 (19,56% pe an).
Contributia №2: rgodovaya = (1 + 0,1) 21 = 0,21 (21% pe an).
(În acest ultim caz, r = 0,1 ca rata dobânzii pe parcursul unei perioade de încărcare (jumătate) este de 10%, iar numărul perioadelor n = 2. Din anul avem două semiperioadă și dobânda se calculează de două ori pe an).
După cum puteți vedea, în acest caz, №2 contribuție a fost mai favorabilă decât contribuția №1.
Dacă știm valoarea curentă a investiției (PV), valoarea viitoare a investițiilor (FV), precum și numărul de perioade (n) - adică numărul de ani, este posibil să se deducă formula de calcul al procentului anual.
În primul rând, derivă din deja cunoscut pentru a ne formula de calcul rata de simplu și compus interes de interes exprimat în zecimal:
Rata dobânzii excluzând reinvestit ieșirea din interesul simpla formula FV = PV (1 + nr), din care rata dobânzii este simplu Formula №8:
Rata dobânzii ajustată reinvestit au calculat cu formula dobânzii compuse FV = PV (1 + r) n. din care vom obține prin reforme Formula necesară №9:
Pentru o perioadă de timp unică (când n = 1), formula pentru un procent Formula identic simplu și complex №10:
Este cunoscut faptul că de 3 ani de investiții în sumă inițială de 1000 de euro sa transformat în 1900 EUR. Este necesar să se calculeze rata dobânzii compuse pe veniturile din dobânzi anual.
Astfel, având în vedere:
Am găsit rata anuală de Formula №9: