Pentru a găsi valorile COSX zona, este necesar să se amintească definiția cosinusul.
Cosinusul alpha pe cercul unitate - este abscisa unui punct obținut prin rotirea de la punctul P0 la unghiul alfa.
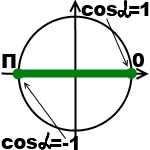
Cea mai mare valoare a cosinusul este egal cu 1, deoarece cea mai mare valoare a lui x pe cercul unitate este 1 (este atins pe dreapta, α = 0).
Prin urmare, domeniul de aplicare al valorilor cosinus - intervalul [-1; 1]. A Valorile cosinus regiune dubla inegalitate poate fi scrisă ca:
Valorile cosinus FIELD nu depind de argumentul (cu excepția cazului când argumentul este o expresie complex cu constrângeri suplimentare asupra valorilor de domeniu și interval):
Astfel, cea mai mică valoare a cos x, cos (), cos 15a (5-11x) etc. este -1;
cea mai mare valoare a cos x, cos (4φ), cos (5x + 3), etc. este 1.
Valorile de câmp ale funcției y = cos x - și intervalul [-1; 1].
Deoarece un număr de chiar nenegativ grad valori regiune pătrat cosinus - intervalul [0, 1] sau
În mod similar, descoperim regiunea cosinus modulul - intervalul [0, 1] sau
În continuare, ia în considerare modul în care, pe baza valorilor limitate ale sinus și cosinus, putem estima valoarea expresiilor trigonometrice și pentru a găsi intervalul funcției.