În § 6 sec. Am observat că paralela, în particular ortogonale, proiectând forme geometrice aranjate aleatoriu în raport cu planul de proiecție, proiectate pe planul caracteristicilor metrice de distorsiune (caracteristici ce pot fi obținute prin măsurarea măsurătorilor unghiulare liniare și). Pentru a putea proiecțiile de a judeca distorsionat metric dimensiunea și forma originalului, este necesar să se cunoască modalitățile de rezolvare a problemelor definiției măsurătorilor unghiulare liniare și nedistorsionat.
Metric numit sarcini care implică găsirea caracteristicilor forme geometrice definite (măsurate) valorile liniare și unghiulare.
Toate sarcinile multiple metrice în cele din urmă reduse la două tipuri: A - problema determinării distanței dintre două puncte; B - pentru a găsi valoarea sarcinilor unghiului dintre două linii care se intersectează.
Prin metrice sunt, de asemenea, probleme privind construcția și unghiul segmentului cu o valoare prescrisă, respectiv, și gradul liniar valoare (radian).
În ciuda faptului că problemele pur metrice sunt rare, este recomandabil vydelyt-le într-un grup independent care să includă acele probleme în care deciziile etapele intermediare trebuie să clarifice relația pozițională dintre forme geometrice.
rezolvarea oricarei probleme de metrice Algoritmul este o proprietate invariantă a proiecției ortogonale, care constă în faptul că orice figură atribuibil plan paralel cu planul de proiecție este proiectat pe această formă congruentă plan, adică. F. (F ⊂ β) ∧ (β || π1) → F ' ≅ F.
Luați în considerare posibilele modalități de rezolvare a problemelor în definirea caracteristicilor metrice de forme geometrice.
A. Determinarea distanțelor.
Rezolvarea problemelor la determinarea unei distanțe între un punct și o linie dreaptă, două linii drepte paralele, un punct și planul, o linie dreaptă și un plan, două planuri care traversează linii drepte, în cele din urmă, se reduce la găsirea distanței dintre două puncte.
Desene Fig. 248 confirmă această afirmație. De asemenea, se observa din aceste cifre că, înainte de a proceda la soluție pentru a determina distanța dintre un punct și o linie dreaptă sau două linii drepte paralele (Fig. 248, și b) este necesar să dețină planul γ perpendicular pe linia l dreaptă, sau să renunțe la o perpendicular dintr-un punct a (a m ∈ sau a ∈ p) pe un plan α (fig. 248, c, d, e, f). De aceea, înainte de a aborda problema la o anumită distanță, pentru a stabili natura și posledo-
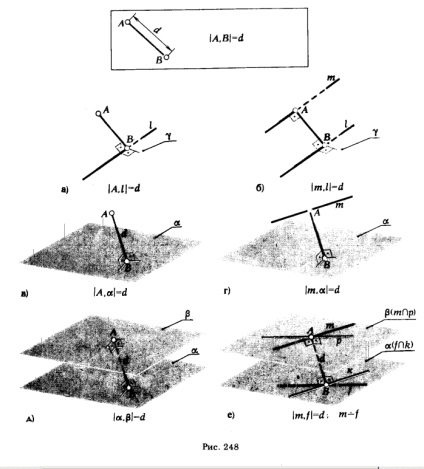
construcții grafice succesive care trebuie efectuate pe diagrama pentru construcția liniilor perpendiculare reciproc, drepte și suprafețe plane.
Construirea de linii perpendiculare reciproc, linii și plane, avioane
Nu este nici o exagerare să spunem că construcția de linii și planuri perpendiculare, împreună cu definirea distanței dintre cele două puncte sunt operațiile grafice de bază pentru rezolvarea problemelor de metrice.
Determinarea o distanță între două puncte
În § 8 Sec. I (vezi. Fig. 50) au arătat o definiție grafică a lungimii [AB], care este o măsură a distanței dintre punctele A și B, prin construirea unui triunghi dreptunghic.
Determinarea o distanță între un punct și o linie dreaptă între liniile paralele
Distanța de la punctul de la linia definită de lungimea segmentului de perpendiculara a scăzut de la un punct pe o linie dreaptă.
Determinarea distanței dintre punctul și planul, o linie dreaptă și un plan între planurile și liniile oblice
Determinarea unei distanțe între 1 - punct și planul; 2 - o linie dreaptă și un plan; 3 - avioane; 4 - linii oblice considerate împreună, ca un algoritm pentru rezolvarea tuturor acestor probleme, în esență, aceleași și constau din construcții geometrice care trebuie efectuate pentru a determina distanța dintre punctul A și dat planul a.
Proiecții de unghiuri plane
Determinarea unghiului de proiecțiile sale plane ortogonale
În secțiunea anterioară a fost menționat faptul că unghiul plat este proiectat pe planul de proiecție fără distorsiuni în cazul în care laturile sale sunt paralele cu acest plan. Această proprietate poate fi luată ca bază pentru elaborarea algoritmului pentru rezolvarea problemei pentru a determina unghiul de proiecțiile sale distorsionate ortogonale.
Determinarea unghiului dintre linia dreaptă și planul
Determinarea unghiului dintre linia dreaptă și un plan, două planuri care traversează linii drepte, este redusă pentru a găsi unghiul dintre cele două linii drepte.
Determinarea unghiului dintre planele
Acesta măsoară unghiul dintre cele două planuri este unghiul liniar format din două drepte - secțiuni, acest unghi se confruntă cu un plan perpendicular pe marginea lor.
Determinarea unghiului oblic între drepte
Între unghiul de înclinare este unghiul plat drept care se formează între liniile drepte trasate dintr-un punct arbitrar în spațiu de date paralele oblic linii.