Prin urmare, mișcarea unui corp este determinată de forța exercitată asupra corpului de către forțele externe fi și momente ale acestor forțe Mi. Momente pot fi luate în raport cu orice staționar sau în mișcare fără axa de accelerație (în raport cu aceeași axă este luată și momentul de inerție I), Luând momentele forțelor exterioare în jurul unei axe care se deplasează cu accelerație, noi, în esență, să scrie ecuația (41.2), într-un cadru non-inerțial de referință , în acest caz, în plus față de forțele exterioare aplicate corpului, trebuie să luăm în considerare forțele de inerție și momentele.
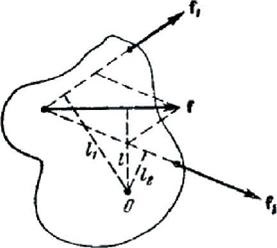
forța punctul de aplicare fi care acționează asupra corpului, poate fi deplasat de-a lungul liniilor de acțiunile lor, pentru că nici suma, nici momentele Mi nu se schimbă (atunci când transportă forța de-a lungul liniilor de acțiune cu privire la orice punct al umărului nu se schimba). Efectuarea un astfel de transfer, este posibil să se înlocuiască mai multe forțe o forță echivalentă cu impactul exercitat asupra mișcării corpului. De exemplu, două forțe f 1 și f 2. se află în același plan (fig. 108), ele pot fi înlocuite cu o forță echivalentă f, punctul în care aplicația poate fi, de asemenea, selectate în mod aleatoriu pe direcția de-a lungul căreia operează.
Totalitatea care acționează asupra organismului poate fi înlocuit cu forțe paralele rezultanta lor egală cu suma tuturor forțelor aplicate la punctul corpului astfel încât punctul său este egal cu suma momentelor individuale ale forțelor.
Găsim rezultanta forțelor de gravitație. Gravitatea aplicată tuturor elementelor unui corp rigid, forța care acționează pe unitatea de greutate # 916; mi. este # 916; mi g. Suma acestor forțe este egală cu P = mg. Momentul total de gravitate cu privire la orice punct O este
unde RI - vector rază determinarea poziției # 916; mi raport cu punctul O. Transferarea factor scalar # 916; mi al doilea factor în primul și retrograda factor comun pentru g semnul sumei, obținem:
Dar suma între paranteze, este produsul masa m a corpului pe raza vectorului rc C. Prin urmare, centrul de masă
t. e, momentul total al forțelor de greutate în raport cu orice punct coincide cu punctul forte mg aplicat la punctul C.
Astfel, forța rezultantă gravitațională este egală cu P = mg și aplicată pe centrul de inerție al corpului.
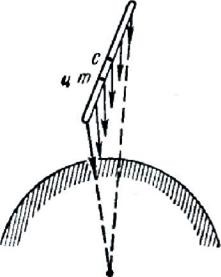
De la (41,3), că punctul de greutate în raport cu centrul de inerție este egal cu zero (în acest caz, rc = 0). Punctul despre care cuplul este zero gravitație, numit centrul de greutate al corpului. După cum sa menționat deja în §23, centrul de greutate coincide cu centrul de masă al corpului. Cu toate acestea, această afirmație este adevărată numai în cazul în care domeniul forțelor gravitaționale în cadrul acestui organism pot fi considerate uniforme, t. E. Atunci când forțele aplicate diferitelor mase elementare, au aceeași direcție și sunt proporționale cu masa. Această condiție este îndeplinită pentru organism, ale cărui dimensiuni sunt mult mai mici decât dimensiunea globului. În cazul în care dimensiunea este comparabilă cu mărimea Pământului, centrul de greutate și centrul de masă este, în general vorbind, nu coincid. Să ilustrăm acest lucru cu un exemplu simplu. Uniformă tijă lungă este în apropierea Pământului (Fig. 109). Cu acest aranjament, tija, așa cum se arată, forțele gravitaționale aplicate diferitelor elemente sunt aproximativ paralele. Amploarea forței aplicate echivalează cu elemente variază în funcție de distanța de la pământ prin lege (r - distanta din centrul elementului pământ). Este evident faptul că centrul de greutate, în acest caz, diferența în raport cu centrul de masă de la sfârșitul barei, mai aproape de Pământ.
Aceeași proprietate ca cea a gravitației (în cazul unui câmp uniform) au forțe de inerție impuse atunci când se analizează mișcarea corpului într-un cadru non-inerțial de referință în mișcare translațional în raport cu sistemul inerțial. Într-adevăr, forțele de inerție aplicate maselor elementare # 916; mi. egală - # 916; mi w 0. t. e. au aceeași direcție și proporțională cu masa (pentru toate punctele sistemului non-inerțial în mișcare translațional, w 0 egal). Repetând argumentele care ne-au condus la formula (41.3), se poate demonstra că forțele de inerție care rezultă este - mw 0 (m - greutate) și este aplicată în centrul de inerție.
În raport cu axa asociată cu deplasarea progresiv un cadru non-inerțial de referință (de ex. E. Axa, se deplasează progresiv în cadrul inerțial) și care trece prin centrul corpului în masă, momentul forțelor de inerție este egal cu zero (rezultate forțele de inerție în acest caz, după cum am văzut, este aplicat la centru inerție). Prin urmare, ecuația (41.2) poate fi scrisă în raport cu această axă, fără a ține cont forțele de inerție. Subliniem încă o dată că acest lucru se poate face numai în raport cu axa care trece prin centrul de inerție și nu se schimbă direcția lor (care nu se rotește) în raport cu un sistem de referință inerțial. Atunci când o astfel axă de mișcare plană este axa care trece prin centrul de masă și perpendicular pe planul în care are loc mișcarea.
condiții de echilibru solide. Corpul poate rămâne în stare latentă în cazul în care nu există motive care duc la apariția mișcării de translație sau de rotație, în conformitate cu (41.1) și (41.2), este necesar și suficient ca au fost îndeplinite următoarele două condiții:
1) Suma tuturor forțelor externe aplicate corpului, ar trebui să fie zero:
În practică, este suficient ca condiție (41.5) deține pentru trei axe fixe care nu se află într-un singur plan (de exemplu, axele de coordonate x, y și z). Apoi va fi valabilă pentru orice altă axă.
Ecuațiile (41.4) și (41.5) și un corp rigid sunt condițiile de echilibru.
Exemple de aplicare a legilor mecanicii solide
Exemplul 1: (. 110 Fig) Dana fascicul omogen, care se află pe două suporturi determină reacțiile de sprijin f 1 și f 2.
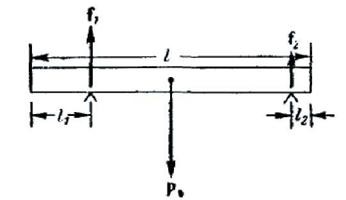
Forța rezultantă de gravitație este aplicată P și centrul de inerție. Fasciculul este fixat. Prin urmare, în conformitate cu (41.4), suma forțelor F, f 1 și f 2 trebuie să fie zero. Rezultă că
unde P, f 1 și f 2 - modulul este putere.
Momentul rezultat al forțelor care acționează asupra fasciculului în jurul oricărei axe trebuie să fie egală cu zero, în special, trebuie să fie zero moment despre punctul de sprijin din stânga, care dă (a se vedea (41.5).):
Avem două ecuații cu necunoscute f 1 și f 2. Rezolvarea ei, găsim:
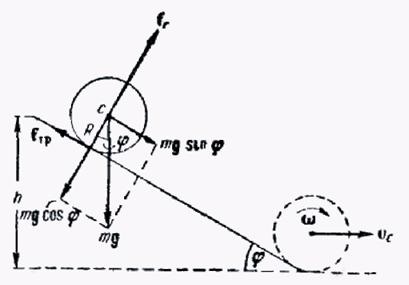
Exemplul 2: Omogen raza cilindrului R și masa m rolele fără alunecarea pe un plan înclinat. planul de unghiul de înclinare este egal cu (Fig. 1l.l), iar înălțimea h (h >> R). Pornirea vitezei cilindrului este zero. Găsiți centrul vitezei de masă și viteza unghiulară de rotație a cilindrului, în punctul de ieșire cilindru pe o porțiune orizontală.
Vom da două opțiuni.
Soluții modul 1st. Cilindrul se va deplasa sub influența a trei forțe: F = mg. forța de frecare f rp și reacțiile fr înclinat avionul. reacție fr potrivit treia legea lui Newton este egal modulo normală forță component P având o magnitudine cos mg # 966; .
Frecarea între cilindru și suprafața înclinată are loc la punctele de contact. Pe măsură ce aceste puncte cilindrului, la fiecare dată încă
(Acestea formează axa de rotație instantanee), forța de frecare în cauză, va fi o forță de frecare statică. După cum se cunoaște din § 19, forța de frecare statică poate avea o magnitudine în intervalul de la zero la o valoare maximă ƒ0. este determinată de produsul coeficientului de frecare la forța de presiune normală, presate unul față de celălalt corp de împerechere (ƒ0 = KMG cos # 966;). În acest caz, forța de frecare are o valoare astfel încât nu a existat nici o alunecare. Alunecare de rulare a cilindrului de-a lungul unui plan să lipsească, cu condiția ca viteza liniară a punctelor de contact este egal cu zero, care, la rândul său, se efectuează în cazul în care viteza centrului de inerție # 965; c este în fiecare moment viteza unghiulară de rotație a cilindrului # 969;, înmulțită cu raza cilindrului R:
În ecuația (41.2), scrisă în raport cu axa cilindrului este diferit de doar un cuplu de frecare zero. Forțele rămase, inclusiv forțele de inerție rezultate au direcția care trece prin axa cilindrului, astfel încât momentele lor despre această axă sunt egale cu zero. Astfel, ecuația (40.2) poate fi scrisă astfel:
Acum, că știm amploarea forței de frecare statică (41.10) furnizarea de rulare fără cilindru de alunecare, poate fi stabilită o condiție de rulare sub care este posibilă. Pentru rulare fără forță (41.10) de alunecare nu trebuie să depășească restul maximă ƒ0 forță de frecare. , după cum am văzut, pentru că egalitatea KMG # 966;:
Prin urmare, se pare că
În cazul în care panta planului # 966; depășește de trei ori valoarea coeficientului de frecare statică între cilindru și nu poate avea loc fără alunecarea laminarea avionul.
Din (41,11), centrul de masă se mută cilindru cu accelerație uniformă. știind accelerarea # 969; s. puteți găsi timpul cilindrului de rulare T ck. t. e. în momentul în care butelia va lua o cale egală cu h / păcat # 966;. În acest fel în legătură cu # 969; c și t c * de relația:
de unde, înlocuind valoarea (41,11), pentru # 969; c. obținem:
De data aceasta ca # 969; c. Ea nu depinde de masa și raza cilindrului [2]; este determinată numai de unghiul de înclinare a planului # 966; iar diferenta de nivel h de marginile sale.
centrul de viteză în masă la ieșirea din cilindru să fie egală cu porțiunea orizontală
și viteza unghiulară a cilindrului
Rețineți că forța de frecare (41.10), se lucrează pe cilindru nu funcționează la fel de bine ca și punctele cilindrului la care se aplică această forță, fiecare cu palete în timp.
Pentru planul orizontal (# 966 = 0) prin (41,11) și (41,12) se obține că cilindrul dacă acesta informează în prealabil unele translațională și adecvate (astfel încât nu există nici o alunecare) viteza unghiulară se va deplasa fără accelerație. De fapt, mișcarea va fi lentă. Această decelerare este determinată, forța de frecare de rulare, care este direcționată, astfel încât momentul său reduce viteza unghiulară # 969;, iar forța în sine determină o corespunzătoare (din nou, astfel încât nu au existat alunecare) încetinire în centrul de masă. Forța de frecare de rulare acționează negativ asupra corpului de rulare.
În rezolvarea problemei de rulare a cilindrului, cu o frecare plan înclinat de rulare, ne-am neglijat.
Metoda soluție 2. Deoarece forța de frecare nu efectuează munca (frecare de rostogolire este neglijată), energia totală a cilindrului rămâne constantă. La momentul inițial al energiei cinetice este zero, energia potențială este MGH, la sfârșitul rulare a energiei potențiale devine egală cu zero, dar există o energie cinetică egală cu [vezi. (40,9)]
nici Deoarece nu există alunecare, # 965; s și # 969; sunt legate. Substituind în expresia pentru energia cinetică și. obținem:
Energia totală la începutul și la sfârșitul de rulare trebuie să fie același:
și viteza unghiulară
Exemplul 3: masa corporala m supuse într-o perioadă foarte scurtă de timp # 8710; t acțiune a forței constante f. Tot restul timpului, cu excepția diferenței # 8710; T. aceasta nu afectează nici organismului. Până la mesajul corpului puls f # 8710; t se bazează. Determina cum să se miște corpul după forța încetează.
Ecuația (41.1), în acest caz, are forma