docent
Cernev Dmitriy Alekseevich
Pas cu pas detaliu (programarea descendentă sau descendentă dezvoltare)
rafinament etapizată este un proces simplu, presupunem-Ai-conductive expresie originală logica modulului în termeni de ipotetice-ches-o singură limbă (condiționată) foarte înalt nivel urmat detaliu fiecare propoziție în termenii unui limbaj de nivel inferior, atâta timp cât în cele din urmă nu a atins nivelul utilizat de limba programului-TION. Este demn de amintit: cea mai mică limba conține detaliile, nivelul mai ridicat. Acesta poate fi considerat ca limba de cel mai înalt nivel al vorbirii umane obișnuite și limba scăzută - limbaj mașină.
Pe parcursul procesului, pas cu pas detaliu logica de proces este exprimat de constructe de bază de programare structurate.
Avantajul granularitate incrementală este că permite proiectantului să organizeze argumentele tale. La fiecare pas, avem de-a face cu o sarcină elementară.
Considerăm că această metodă un exemplu specific.
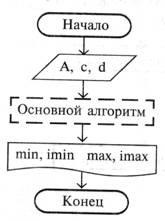
SCOP. Având în vedere dimensiunea matrice 10 x 10 elemente. Pentru fiecare coloană ith dintre elementele situate deasupra primul zero și valorile de care se află în intervalul [c, d], găsiți cele mai mari și mai mici elemente și numărul acestora în șir. Dacă elementul zero al coloanei nu este prezent, întreaga coloană este procesată.
Planul de a rezolva problema
2. Algoritmul de bază (de ciclu coloană).
3. coloană de procesare (buclă internă).
4. Elementele de procesare ale matricei.
5. Găsiți cele mai mari și mai mici elemente din coloană.
6. Prelucrarea operatorilor ciclurilor inițiale și terminale.
7. Optimizarea și programul resurfacing.
A (10, 10) - matricea inițială.
C și D - limita intervalului.
m ax (10) și min (10) - Vectori care conțin valori maxime și minime ale fiecărei coloane a matricei originale.
Imax (l 0) și Imin (l 0) - șiruri de numere de linie în care se găsesc rezultatele, respectiv, iar valorile mai mici greatest NAI din coloană.
a) Primul pas detaliere IO.
A: ARRAY [1..10,1..10] REAL; (* Inițială * matrice)
C. D. REAL; (* Slot limite *)
I. J. INTEGER; (* Rânduri și coloane non *)
MAX. MIN. ARRAY [1..10] DE REAL; (* Valori mai mari și *)
IMAX. IMIN. ARRAY [1..10] integer; (* Și numerele lor de linie *)
Căutați cele mai mari și mai mici elemente din coloana a matricei A, și numerele lor în linie.
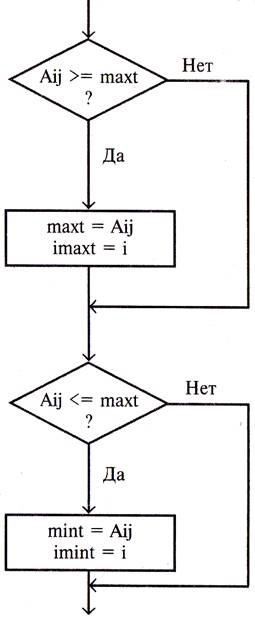
DACĂ A [I, J]> = MAXT începe apoi MAXT: = A [I, J]; IMAXT: = I; END;
DACĂ A [I, J]<= MINT THEN BEGIN MINT:= A[I, J]; IMINT:= I; END;
Au fost introduse noi variabile: Macht și MINT, IMAXT și IMINT. care urmează să fie incluse în descrierea variabilelor cu atribuirea de tip REAL și respectiv INTEGER.
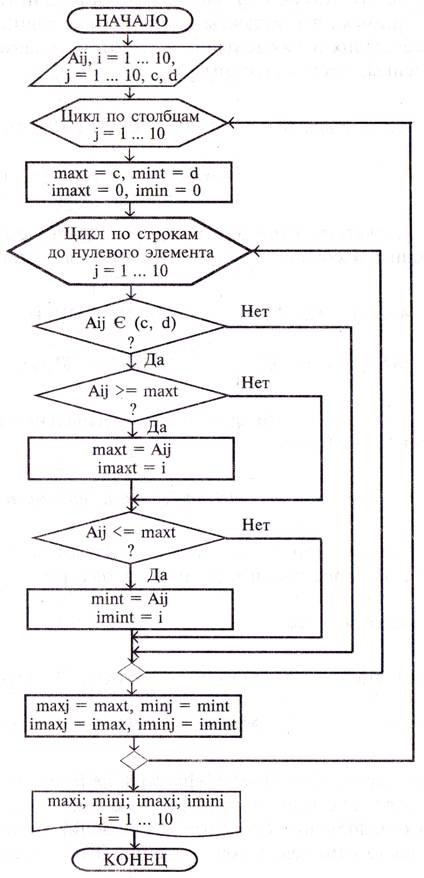
e) Al șaselea pas. Declarațiile inițiale și finale.
Ne indreptam din interior spre exterior cicluri și a vedea ceea ce ai nevoie pentru a lucra cicluri.
este necesar pentru funcționarea buclei interioare a Macht MINT și a avut o anumită valoare, și ce să facă în prima etapă, în absența elementelor de coloană în intervalul (a, d)?
Presupunem că, în acest caz, codurile sunt zero, iar valorile maxime și minime ale elementelor care intră în matricele de ieșire sunt nesemnificative.
Macht: = C; MINT: = D;
M Intră pe chat: = 0; IMINT. = 0;
Rezultatele acestui ciclu, este necesar să se trimită în J - elemente de e-al rezultantei matrice, astfel încât declarațiile finale sunt după cum urmează:
MAX [J]: = Macht; IMAX [J]: = M ChAT;
MIN [J]: = MINT; IMIN [J]: = IMINT;
Pentru ciclul coloanelor nu sunt opera-Tori inițială și finală nu este necesară.
După primirea programului, puteți face pentru a îmbunătăți, astfel încât devine mai scurtă sau alerga mai repede.
utilizați MAX (J), MIN (J), IMAX (J), IMIN (J)
în schimb Macht. MINT, IMAXT, IMINT,
operatorii de linie finală nu sunt necesare, dar programul va fi realizat mai mult timp (deși textul acesteia va fi redusă), deoarece operațiune ESTATE-titsya „Apel către elementul de matrice“ - o destul de lung, din punct de vedere al calculatorului, operațiunea.
Este posibil, de asemenea, optimizarea pași.
A: ARRAY [1..10, 1..10] DE REAL; (* Inițială * matrice)
C. D. REAL; (* Slot limite *)
I. J. INTEGER; (* Rânduri Non și coloane din matricea A *)
MAX. MIN. ARRAY [1..10] DE REAL; (* Valori mai mari și *)
IMAX. IMIN. ARRAY [1..10] integer; (* Și numerele lor de linie *)
MAXT. MINT. REAL; (* Variabile temporare, și cele mai multe *)
(* Mici valori de element *)
IMAXT. IMINT. INTEGER; (* Și numărul lor în coloana *)
Writeln ( „Introduceți elementele matricei:“);
PENTRU I: = l până la 10 DO
PENTRU J: = 1 TO 10 DO READ (A [I, J]); writeln;
Write ( „Introduceți limita intervalului“); Readln (C, D);
PENTRU J: = l 10 DO (* coloane de prelucrare a matricei A *)
IMAXT: = 0; IMINT: = 0; MINT: = C; MINT: = D;
(* Elemente de coloane Prelucrarea matricei A *)
PENTRU I: = l 10 DO WHILE A [I, J] # 0 DO
IF (C<=A[I, J]) AND (A[I, J]<= D) THEN
(* Element de matrice face parte din segmentul CD. *)
DACĂ A [I, J]> = MAXT (* cel mai mare element al matricei. *)
BEGIN APOI MAXT: = A [I, J]; IMAXT: = I; END;
IF [I. J]<= MINT (* Элемент матрицы наименьший? *)
BEGIN APOI MINT: = A [I, J]; IMINT: = I; END;
MAX [J]: = MAXT; MIN [J]: = MINT;
IMAX [J]: = IMAXT; IMIN [J]: = IMINT;
PENTRU I: = l până la 10 DO writeln ( 'MIN =', MIN [I], 'numărul său', IMIN [I],
'; MAX =', MAX [I], 'numărul său', I MAX | I]);




Material Site-ul este un instrument electronic
pe tema „Software Engineering“
pentru a ajuta elevii TUIT.