Definiții de bază Laplace proprietăți transformare Formula Duhamel

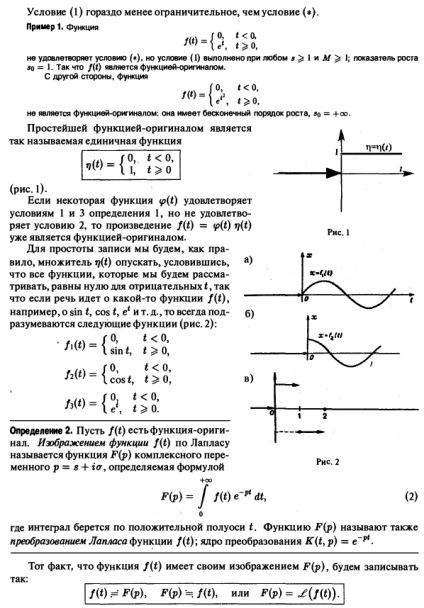


















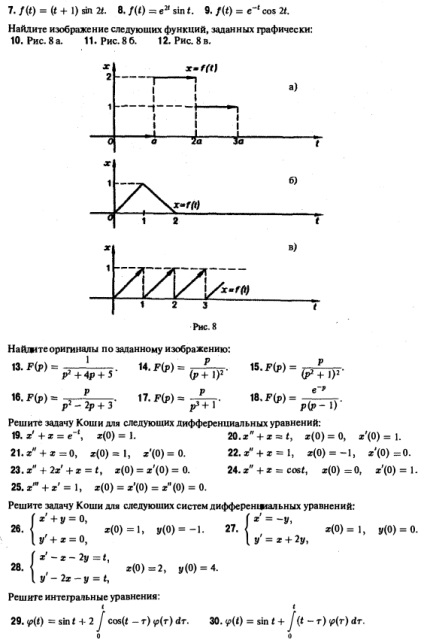

Mai devreme ne-am uitat la transformata Fourier integrală cu kernel-ul K (t, Q = f transformata Fourier incomodă care trebuie să fie starea integrabilitatea absolută a funcției f (t) pe axa întregii t, transformata Laplace vă permite să se elibereze de această limitare. Definiție 1. Funktsiey- va nazyvatvsyakuyu inițial evaluate complex funcția f (t) deystvitsl nogo argument t, yushuyu îndeplinește următoarele condiții: 1. f (t) este continuă pe tot parcursul axei t, în afară de puncte individuale în care f (t) este prima discontinuitatea ordine, în care nakazhdom termina intervaleosi * t kihtochek mozhetbyt doar un număr finit, 2. funcția f (t) este zero pentru valori negative ale t, f (t) = 0 pentru t 3 cu creșterea modulului f (t) nu crește funcția mai rapidă exponențială, adică există numărul M .. > 0 și s astfel încât pentru orice t este clar că, dacă inegalitatea (1) are loc pentru unele s = aj, atunci acesta va fi executat și pentru fiecare 82> 8]. infima s0 toate numerele de „a = infs, pentru care inegalitatea (1) se numește funcția de indicator de creștere f (t). Notă. În general, inegalitatea nu deține, dar în cazul în care estimarea e> 0 - oricând. Astfel, funcția are o rată de creștere = B0 Pentru inegalitatea ei \ t \ ^ M * V ^ 0 nu deține, dar inegalitatea | f | * Mei. Condiția (1) este mult mai puțin restrictivă decât condiția (*). Exemplul 1. Funcția nu satisface condiția ( „), dar condiția (1) este valabil pentru orice s ^ I și A / ^ I; rata de creștere de 5 ° = • • Care este funcția inițială. Pe de altă parte, funcția nu este o funcție inițială: are o creștere ordine infinit „, a = + oo. Cea mai simplă funcție, originalul este o funcție de unitate de așa-numita Dacă o funcție îndeplinește condițiile 1 și 3 din Definiție 1, dar nu îndeplinește condiția 2, produsul este deja o caracteristică inițială. Pentru simplificare, vom, de regulă, rj (t) factor este redus, cu condiția ca toate caracteristicile pe care le considerăm egală cu zero pentru t negativ, dat fiind că, atunci când este vorba de o anumită funcție f (t), de exemplu, despre ty păcat cos t, el etc., se înțelege întotdeauna următoarele caracteristici (Figura 2):. .. n = n (. 0 Figura 1 Definiție 2. Fie f p) = e