paradox matematic poate fi definit ca adevăr. astfel încât contrar experienței noastre, intuiția și bunul simț că este greu de crezut, chiar și după ce am pas cu pas pentru a urmări toate dovezile sale. sofistică matematică numit nici o declarație mai puțin surprinzătoare dovezi că, în contrast cu dovezile de paradoxuri mint erori invizibile, și, uneori, destul de subtile. În orice domeniu de matematică - de la aritmetică simplă la topologia modernă set-teoretic - au psevdodokazatelstva lor, sofistică lor. În cele mai bune dintre aceste argumente cu greșeală, mascată cu grijă permit să vină la constatările cele mai incredibile.
Prima noastră eroare este extrem de elementar. Noi preceadă-l paradox amuzant, exemplul pe care marele matematician german David Hilbert îi plăcea să explice proprietățile neobișnuite ale cel mai mic dintre ordinal „Aleph-zero.“ După ce proprietarul unui hotel magnific cu un număr infinit, dar numărabil de camere de hotel, dintre care niciunul nu a fost liberă, a fost necesar să se adopte un nou invitat. Proprietarul a ieșit din situația este foarte simplu: fiecare dintre invitații săi, el a mutat la camera, care a fost un număr unu mai mare decât numărul anterior al camerei, care rezultă în n-lea locuitor al camerei sa mutat la (n + 1) lea și a lansat pentru prima oaspete nou cameră. Cum se poate face un proprietar în cazul în care ajunge la infinit mulți oaspeți noi? Nu a fost confundat, gazda relochează toate fostele oaspeții săi în camere cu un număr dublu mare (oaspete al camerei 1 se mută la camera 2, oaspetele din camera 2 - camera 4, oaspetele din camera 3 - camera 6, oaspetele din camera 4 - în camera 8, și așa mai departe. d.) și plasează noii veniți în camere eliberat cu numere impare.
Dar trebuie să fie proprietarul să aibă un număr numărabil de camere pentru a găzdui oaspeți noi? În Stishov de mai jos, luate de la o revista britanica, publicat in ultimul secol, se spune despre hangiului viclean, care a fost capabil de a găzdui nouă camere zece oaspeți, astfel încât fiecare dintre ele are o cameră separată.
Au existat zece excentrici,
Acești sateliți obosit,
Asta a decis să bat la ușă
Tavernele „tip de treabă.“
- Dă-mi drumul, maestru, Lodge,
Nu va fi la o pierdere,
Am fost doar o noapte pentru a dormi,
Am fost înmuiate pe piele.
Proprietarul oaspeții au fost încântați
Dar probleme din loc:
Doar nouă camere ea
Și doar nouă paturi.
- Voi oferi opt persoane
Pat onoare să-și onoreze,
Și cei doi trebuie să doarmă prin noapte
În același pat împreună.
Doar a spus el, și plânge imediat
Din față roșie de furie:
Nici unul din toate cele zece
El nu vrea să facă loc.
Cât de rece pasiunile fervoare,
cele moderată emoție?
Dar proprietarul a fost necinstiți vechi
Sau se îndoiesc.
Primele două călătorii încă
Pentru a nu fi judecat sever,
El a cerut să meargă la numărul „A“
Și așteptați un pic.
Am dormit în a treia „B“, a patra în „B“
„G“ a dormit toată noaptea, a cincea noastră,
"D", "E", "F", "3", B găsit
De la al șaselea al nouălea.
Apoi, întorcându-se înapoi la „A“
În cazul în care așteptare pentru el două,
El este cheia „I“ a fost fericit pentru a da
erou al X-lea.
Deși mulți ani au trecut de atunci,
Nu este clar pentru oricine,
Cum ar putea postul de master
Oaspeții unul câte unul.
aritmetica Ile vechi
Sau un miracol înaintea noastră,
Pentru a înțelege ce, cum și de ce,
Încercați să faceți.
Un exemplu de mai subțire este următoarea matematică sofism „algebrică„dovada că orice număr precum și un număr mai mic b.
Să începem cu egalitatea
Înmulțind ambele părți de a - b. obținem
Se transferă asul în partea stângă:
și luat:
Impartind ambele părți de a - b - c. găsi
QED.
Multe probleme așteaptă cel care se referă din greșeală la unitatea imaginară i (rădăcina pătrată a -1). Acest lucru este demonstrat de cel puțin următoarea uimitoare „dovada“ a egalității 1 = -1:
Fig. 82. Triunghiul Kerry.
În planimetrie cele mai multe dovezi false cu privire la utilizarea de desene incorecte. Luați în considerare, de exemplu, uimitor „dovada“ că zona din partea din față a poligonului. tăiat din hârtie este diferită de zona părții din spate a aceluiași poligon. Acest „dovezi“, a fost inventat de psihiatrul L. Vosburgh Lyons, foloseste un principiu curios descoperit P. Kerry.
În primul rând pentru a trage foaia de hârtie în triunghiul celulă a cărei suprafață este egală cu 60 de celule (Fig. 82) și a croielii de-a lungul liniilor prezentate în figura superioară. Revenind triunghiul la cealaltă parte și în afara ei un triunghi prezentat în Fig. 82 în mijloc, constatăm că, în centrul noului gaura triunghi a apărut în zona de 2 celule. Cu alte cuvinte, suprafața totală a originalului piese de triunghi îngustarea a scăzut la 58 celule! Revenind din nou (cu fața în sus), doar trei dintre triunghiului inițial, putem face din toate cele șase părți ale figurii prezentată în Fig. 82 de mai jos. Suprafața sa este egală cu 59 de celule. Ceva e în neregulă aici, este clar, dar ce anume?
Teoria probabilităților este plină de credibil, dar nu în mod logic impecabil raționamentul. Să presupunem că ați întâlnit cu prietenul său Ioan, și că fiecare dintre voi este cravata că soția ta ia dat de Crăciun. Începi să argumenteze despre a cărui cravată este costisitoare, iar în cele din urmă decide să meargă la magazinul de unde au fost cumpărate legături și de a afla cât de mult fiecare dintre ele. Cine câștigă (a cărui cravată ar fi mai scump) pariu cu condiția trebuie să dea ratat cravată să se înmoaie amărăciunea înfrângerii.
Tu vorbești așa: „Șansele de a câștiga și a pierde în același mine. Câștigătoare, am sărăci o sumă egală cu costul cravata mea. Dupa ce a pierdut, voi primi cravată mai scumpe. Prin urmare, pentru a face un pariu. Mi-ar fi într-o poziție mai bună decât prietenul meu. "
Desigur. nu este nimic de oprire pentru a vorbi cu John în același mod. Poate ambele părți, a făcut un pariu, au avantajul reciproc?
Unul dintre cele mai impresionante paradox topologie constă în faptul că pilier (suprafața gogoașă), în cazul în care suprafața sa se intinda (nu ruperea în timpul acestei) poate fi întors pe dos față de orice gaura arbitrar de mici. Nu există nici o problemă aici. Dar, în cazul în care este într-adevăr posibil pilier de a transforma pe dos, este necesar să se acorde atenție încă o, poate chiar mai remarcabil fapt.
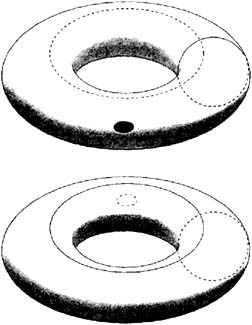
Fig. 83. În cazul în care pilier intoarsa pe dos, se pare că inelele pictate pe suprafață, sunt decuplate.
Pe partea exterioară a torului trage meridianul (Fig. 83, sus). Pe partea interioară a aceluiași comportament torusului paralel. Ambele aceste cercuri sunt în mod evident, legate între ele. Deșurubați acum pilier interior printr-o gaură în suprafață. După cum se poate observa din figura de jos, primul cerc merge spre interior de la suprafața exterioară a torului, iar celălalt - spre exterior, iar ambele cercuri vor fi decuplată! Evident. că încalcă legea fundamentală topologic care prevede: separa cele două curbe închise cuplate se poate rupe doar una dintre curbele și tragerea prin locul al doilea decalaj.
În ultimul nostru sofism, care este preluată din teoria elementară a numerelor, va fi despre meritele relative ale numerelor „interesante“. Desigur. Numerele pot fi de interes din perspective diferite. Deci, pentru George Moore, când a scris celebra sa odă femeie de treizeci de ani, un interes deosebit a fost numărul de 30 - Moore a crezut că la această vârstă, femeile căsătorite sunt deosebit de atractive. Pentru expert în teoria numerelor reprezintă numărul 30 apare. chiar mai interesant, pentru că este cea mai mare dintre numere, cu proprietatea că toate numerele mai mici care nu are factori comuni cu ei, pro-sty. Numărul de 15873, de asemenea, este interesant: atunci când este multiplicată de somn-provo pe orice figură, care este, pe oricare dintre numerele de la 1 la 9, apoi 7, atunci rezultatul va consta din repetiții selectate pentru prima multiplicare a numerelor. Chiar și proprietăți mai uimitoare are un număr de 142 857: înmulțirea cu numere de la 1 la 6, veți primi o permutare ciclică a acelorași șase numere.
Se pune întrebarea dacă există un număr neinteresante? Cu ajutorul unui raționament elementar nu este dificil de a dovedi că nu există nici un număr neinteresante. În cazul în care există numere plictisitoare, atunci toate numerele pot fi împărțite în două clase: numărul de numere interesante și-esting neinte, plictisitoare. Într-o varietate de numere neinteresante ar exista un singur număr, care ar fi cel mai mic dintre toate numerele neinteresante. Dar, cel mai mic dintre toate numerele neinteresante - acesta este numărul în sine este interesant. Prin urmare, ne-ar trebui să-l eliminați din setul de numere neinteresante și traduce într-un alt set. În setul rămas, la rândul său, s-ar fi găsit cel mai mic număr. Prin repetarea acestui proces pentru o lungă perioadă de timp, poate fi interesant la orice număr în neinteresante.
Cea mai mare îngrijorare cititorii livrate sofistică cu torusului la interior spre exterior. Thor este într-adevăr posibil să se transforme în interior, dar își schimbă orientarea. Ca rezultat, ambele cercuri sunt interschimbate și rămân în angajament. Dacă ați tăiat partea de jos a ciorapului și coase capetele tubului, turn-Khodnev este mai mare decât modelul torusului. fire Acesta de culori diferite pot fi pro-lash meridiane și paralele. Astfel de torus transforma cu ușurință printr-o gaură în suprafață, perfect limpede toate PROIS merge cu meridianul și paralel.
Algebra - Una dintre cele mai mari zone de matematică, deținute împreună cu aritmetica și geometria din cele mai vechi ramuri ale acestei științe. Obiectivele și metodele de A. se distinge de alte ramuri ale matematicii au fost create treptat, începând cu cele mai vechi timpuri. Algebra a apărut sub influența nevoile practicii sociale, ca urmare a unei căutări de metode comune pentru rezolvarea problemelor aritmetice de același tip. Aceste tehnici sunt, de obicei, în formularea și soluția de ecuații. Ie algebrică sofistică - erori în mod deliberat ascunse în ecuațiile și expresiile numerice.
1. „Două numere naturale diferite egal“
Noi rezolva sistemul de două ecuații:
Facem acest lucru prin substituirea 2-lea moment al ecuației 1, obținem x 8 + x = 6, 8 unde da = 6
În cazul în care este eroarea.
2. „Un număr negativ este mai mare decât pozitiv.“
Să luăm două numere pozitive a și c. Să comparăm două atitudini:
și / -c și -a / c
Ele sunt egale, deoarece fiecare dintre ele este egal cu - (a / c). Puteți face o proporție: a / -c = -a / c
Dar, în cazul în care proporția de primul termen al primului raport este mai mare decât mai târziu, primul termen al doilea raport este, de asemenea, mai mare decât următorul său. În cazul nostru, a> c, urmatoarea quently, trebuie să fie s> c, de exemplu, un număr negativ este mai mare decât pozitiv.
În cazul în care eroarea.
3. „Doi plus doi este egal cu cinci.“
Notăm 4 = a 5 = b, (a + b) / 2 = d. Avem: a + b = 2d, a = 2d-b, 2d-a = b. multiplica ultimele două egalități în părți. Obținem: 2DA-a * a = 2dB-b * b. Inmultiti ambele părți ale ecuației rezultată prin -1 și se adaugă la rezultatele d * d. Avem: un 2-2da + d2 = b2 -2bd + d2, sau (a-d) (a-d) = (b-d) (b-d), în cazul în care a-d =-b d și a = b, adică, 2 * 2 = 5
În cazul în care eroarea.
Pe lângă sofistică matematică. există multe altele, cum ar fi logica, terminologia, psihologice, etc. Pentru a înțelege absurditatea unor astfel de pretenții mai ușor, dar ele nu devin mai puțin interesante din aceasta. Prea multe arata ca sofistică lipsit de sens și scopul jocului cu limba; joc, bazat pe ambiguitatea expresiilor lingvistice, incompletitudine lor, subestimare, în funcție de contextul valorilor lor, etc. Aceste sofisme par deosebit de naiv și frivol.
"Half-gol și pe jumătate plin"
„Half-gol este la fel ca și pe jumătate plin. În cazul în două părți egale, înseamnă, și sunt numere întregi. Prin urmare, gol este la fel ca și pe deplin. "
„Chiar și ciudat“
„5 este 2 + 3 ( "doi și trei"). Doi - numărul este chiar, trei - ciudat, se pare că cinci - numărul și pare și impare. Cinci nu este divizibil cu doi, precum și 2 + 3, atunci cele două numere nu sunt seara! "
„Nu știu ce știi“
„Știi ce vreau să te întreb?“ - „Nu“. - „Știi că virtutea este bun?“ - „Eu știu.“ - „Asta am vrut să te întreb. Și tu, se pare că nu știi ce știi. "
„Medicamente“
„Remediul acceptat de pacient, este bun. A face mai bine este mai bine. Deci, trebuie să luați medicamente cât mai mult posibil. "
„Cea mai rapidă creatura nu este în măsură să ajungă din urmă cu cel mai lent“
Sprinten Ahile nu va depăși lent în mișcare Turtle. Până când el ajunge la broasca țestoasă Ahile, va merge mai departe un pic. El a depăși rapid această distanță, dar țestoasa va lăsa un pic mai înainte. Și așa mai departe la infinit. Ori de câte ori Ahile va ajunge la locul unde a fost înainte de această broască țestoasă, acesta va oferi cel puțin un pic. dar înainte.
„Nu există nici un sfârșit“
Un obiect în mișcare trebuie să ajungă la jumătate din drumul său înainte de a ajunge la final. Apoi, el trebuie să treacă de jumătate din jumătatea rămasă, apoi jumătate a patra parte, etc. la infinit. Subiectul va fi în mod continuu se apropie de punctul final, dar niciodată nu ajunge.
O masă mare de mici, cum ar fi mei de cereale în toamna la sol face întotdeauna un zgomot. Acesta este compus din boabe individuale de zgomot, și, prin urmare, fiecare bob și cea mai mică porțiune din fiecare bob ar trebui să fie în scădere, zgomot Produ-dit. Cu toate acestea, un singur bob cade pe sol complet silențios. În consecință, care se încadrează la cereale medimnov la sol nu trebuia să facă zgomot, deoarece este compus dintr-o multitudine de granule, fiecare dintre care cade tăcut. Încă medimnov de cereale cade de zgomot!
„Poate un magician omnipotentă a crea o piatră care nu se poate ridica?“
Daca nu se poate - atunci el nu este atotputernic. Dacă se poate - deci, nu este atotputernic, deoarece el nu se poate ridica această piatră. „Fa un pahar plin gol Raven?“
Da. Utilizați un argument. Să fie un pahar plin cu apă până la jumătate. Apoi, putem spune că paharul este pe jumătate plin de sticlă. pe jumătate goală. Creșterea ambele părți de două ori, am descoperit că un pahar este plin de sticlă goale.
„Sofistăriei Cratilos“
Argumentul dialectician Heraclit, proclamat „totul curge“, a explicat că, în același râu (imaginea naturii) nu pot intra de două ori, pentru cazul în care de intrare vor fi incluse data viitoare, se va scurge apa este alta. Discipolul său Cratilos, a făcut din aprobarea profesorilor alte constatări: în același râu nu poate intra nici măcar o dată, pentru că atâta timp cât introduceți, sa schimbat deja.
Evatl sofistică a luat lecții de la Sofistul Protagoras, cu condiția ca el să plătească taxa numai dacă vei câștiga primul proces. Elev după antrenament nu a luat desfășurarea unui proces și, prin urmare, a considerat el însuși dreptul de a nu plăti taxa. Profesorul a amenințat că va depune o plângere în instanță, spunându-i următoarele: „. Juriul va acorda sau să plătească taxa sau nu vor fi atribuite, în ambele cazuri, va trebui să plătească în primul caz de condamnare judecător, în al doilea caz, în virtutea acordului nostru“. Acesta Evatl a răspuns: „Nu că, în orice alt caz, eu nu plătesc Dacă sunt condamnat să plătească, atunci am pierdut primul proces, nu plătesc din cauza acordului nostru, iar dacă nu pot fi condamnați la plata taxei, eu nu fac. plătească în temeiul unei hotărâri judecătorești. " (Eroare devine clar dacă am pus două întrebări distincte: 1) dacă sunt sau nu să plătească Evatl și 2) dacă termenii contractului executat sau nu).
Exemple de sofistică, formulate în Grecia antică:
„Sitting a stat; care se ridică și costurile; Prin urmare, stând în valoare de ea. "
„Socrate - un om; Oamenii - nu același lucru, că Socrate; Prin urmare, Socrate - este altceva. decât Socrate. "
„Pentru a putea vedea, nu au neapărat un ochi, pentru că fără ochiul drept vom vedea fără a vedea, de asemenea, stânga; cu excepția dreapta și stânga, alții nu au ochi; deci este clar că ochii nu sunt necesare pentru a vedea. "
„Cel care se află, spune despre cazul în cauză sau de a vorbi despre ea; dacă el vorbește despre acest caz, el nu minte; dacă nu vorbește despre acest caz, spune el, de ceva inexistent, și este imposibil să nu numai să mintă despre asta, dar chiar să se gândească și să vorbească. "
„Dacă cineva spune că a rămas, dacă el a fost culcat sau a spune adevărul?“ Presupunerea că el spune adevărul, aceasta va însemna că este adevărat. el a fost culcat (despre acest lucru, spune el), atunci se dovedește că minciuna. Dacă el minte, este tocmai faptul că el admite în mod deschis. Se pare că spune adevărul. "
Exemple de sofistică moderne:
„Unul și același lucru nu poate avea nici o proprietate și nu-l au. Contabilitatea costurilor presupune independența, angajament și responsabilitate. Interesul - nu este, evident, responsabilitatea și responsabilitatea - nu independența. Se pare contrar a ceea ce a fost spus la început, care include o independență autoportant și lipsa de independență, responsabilitate și iresponsabilitate. "
„Societate pe acțiuni, a primit o dată împrumutul de la stat, acum el nu ar trebui să aibă, pentru că a fost diferită: în timpul domniei lui nu era nici unul dintre cei care aplica pentru un credit.“