mișcare de rotație. mișcarea uniformă a punctului de pe circumferința. Vectorul viteză unghiulară. accelerație unghiulară
În mișcare uniform accelerată o particulă se mișcă mereu în același plan format de către vectorul inițial viteza v (0) și accelerația constantă a (dovedesc). Cu toate acestea, este evident că nu orice mișcare plan este uniform accelerată. Exemplul de circulație neravnouskorennogo plat, cunoscut pentru tine de curs de fizica școală - o mișcare circulară uniformă. Să ne uităm la ea aici. Deoarece acest plan mișcare, selectați ca acest plan, planul XY. Am ales originea în centrul circumferinței (fig. 1).
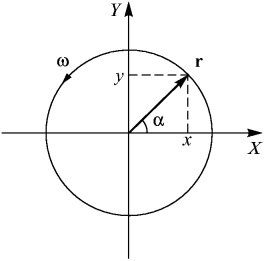
Fig. 1. mișcarea circulară uniformă.
Coordonatele exprimate în funcție de dimensiunea particulelor de rază r și unghiul de circumferință # 945;.
Deoarece mișcarea are loc de-a lungul circumferinței, r este independentă de timp. Funcția de timp este doar unghiul # 945; (T). Derivatul timp a unghiului este numit viteza unghiulară # 969;.
Din compararea acestor două expresii obținem asta. Astfel, vectorul accelerație este antiparalel vectorul r. care este îndreptată spre centru. Ca rezultat, imaginea arată direcțiile vectorilor, așa cum se arată în Fig. 2.
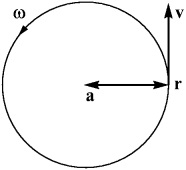
Fig. 2. Raza vectorului, viteza și accelerația unui punct de masă la o mișcare circulară uniformă.
Până în prezent, atunci când se analizează mișcarea de rotație, am operat pe proiecțiile axelor de coordonate. În același timp, este adesea util să aibă relații nu depind de alegerea sistemului de coordonate, sau, așa cum este înregistrat într-o formă de vector. Exemple de astfel de raporturi este expresia pentru poziția și viteza unei particule la o mișcare uniform accelerată (vezi. Curs 2).
Atunci când se analizează mișcarea de rotație am introdus viteza unghiulară # 969; ca derivata a unghiului de rotație # 945;. # 969; = D # 945; / Dt. Să ne întreb acum întrebarea cum magnitudine, scalar sau vectorul este de rotație. La urma urmei, atunci când vorbim despre rândul său, este necesar să se precizeze nu numai magnitudinea unghiului de rotație, dar, de asemenea, în jurul oricărei axe, rotația (rândul său), și în ce direcție (sensul acelor de ceasornic sau în sens invers). In exemplul de mai sus de axa de rotație a fost axa z și, pentru că am folosit un sistem de coordonate dreapta, rotația este sensul acelor de ceasornic (atunci când este privit în direcția pozitivă de-a lungul axei z) (fig. 3).
Fig. 3. Direcția de rotație.
Din acest punct de vedere, unghiul de rotație trebuie să fie o cantitate vectorială. Cu toate acestea, după cum vom vedea în următorul curs, vectorul de rotație unghi arbitrar, în general, govopya nu este. vector de conceptul aplicabil numai în raport cu infinit mici unghiuri de rotație.
De aceea, vorbind despre activarea un anumit unghi mic # 916; # 945;. Ea poate fi aproximată pentru a vorbi despre vectorul # 916; # 945; . valoare egală cu unghiul de rotație și direcția indică direcția axei de rotație, astfel încât rotația este în sens orar sau conform regulii mâinii drepte. În cazul nostru particular, vectorul # 916; # 945; este coliniar cu direcția axei z. Ne întrebăm cum conectat mișcarea unui punct material # 916; r prin rotirea raza vector r la un unghi mic # 916; # 945; (Fig. 4).
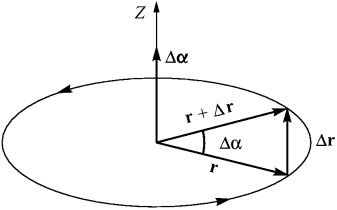
Fig. vector de mișcare 4. Comunicarea cu unghiul de rotație.
Această întrebare este ușor de răspuns, dacă este vorba despre rotatii infinitezimale d # 945; . Apoi, deplasarea infinitezimal și este dr. Valoarea sa (egala cu lungimea corzii) este acum la fel cu lungimea arcului, adică,
iar dr vectorul de direcție coincide cu tangenta, adică perpendicular pe r. Ca rezultat, avem trei vectori reciproc perpendiculare r. dr și d # 945; . formând un dreptaci (fig. 5)
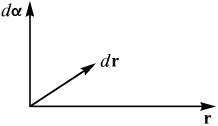
Fig. 5. Orientarea relativă a trei vectori.
și | dr | = | D # 945; | | R |. Cei care amintesc de un curs de școală pe produsul vectorial al vectorilor, înțeles fără dificultate că raportul dorit poate fi scris ca o ecuație vector
Într-adevăr, prin definiție, produsul transversală a doi vectori A [x B] este vectorul
care este orientată perpendicular pe planul în care se află (sau care formează) doi vectori A și B. în afară de acest plan care corespunde regulii de degetul mare (vezi. fig. 6).
Fig. 6. Orientarea tpeh produsului vectorial vektopov.
Magnitudinea vectorului C este egală cu produsul dintre modulii vectorilor prin sinusul unghiului dintre ele:
În cazul nostru, unghiul dintre vectorii d # 945; și r este egal cu 90 °. astfel încât sinusul este egal cu unu. Și, din moment ce, după cum am menționat deja, | dr | = Rd # 945;. vom verifica validitatea dr raportul vector = [d # 945; r ×].
Impartind ambele părți ale acestei ecuații de un timp dt interval infinitezimal. în timpul căreia a existat o schimbare în vectorul r dr. obținem
Cu toate acestea, cantitatea de pe partea stângă, nu este altceva decât o viteză a particulelor v. și derivatul
Se numește vectorul viteză unghiulară. Am introdus pentru prima dată în termeni absoluți, iar acum au arătat că are sens să vorbim despre viteza unghiulară ca vector. Valoarea sa determină mărimea vitezei unghiulare (viteza de rotație, sau viteza schimbării unghiului), iar direcția paralelă cu axa de rotație, și astfel încât să existe o regulă dreapta. Așa că am înțeles
Orientarea acestor tpeh vektopov prezentată în fig. 7.
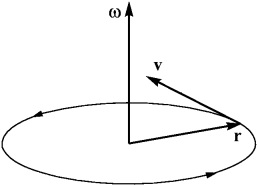
Fig. 7. Orientarea ratei vectorului rază, vectorul viteză și girație.
Pentru a obține accelerația a. este necesar ca ambele părți să ia derivata în raport cu timpul. dacă # 969; în mod constant (atât în mărime și direcție) 1.
adică, accelerația este perpendiculară pe viteza unghiulară # 969; iar viteza de deplasare v. Și din moment ce acesta din urmă este îndreptat tangențial, aceasta înseamnă că accelerația este direcționat fie paralelă cu r. sau antiparalel. Cum anume, puteți afla în formula de mai sus, înlocuind o valoare v. 2
Deoarece în exemplul nostru, la începutul coordonatelor în tsent.pe SELECT okpuzhnosti, viteza unghiulară # 969; și vectorul r raza perpendicular unul pe altul și, în consecință, produsul lor scalar este zero (în general, după cum vom vedea, în nici un caz întotdeauna) și obținem
vectori adică antiparalel o și r (amintiți termenul „accelerația centripetă“). În mărime, acestea sunt: | o | = # 969; 2 | r |. de exemplu, au un rezultat familiar.
Ați putea întreba de ce avem nevoie pentru a face față cu vectorul și un produs dublu-vector, dacă am demontat deja mișcarea circulară, diferențierea în raport cu timpul proiecției unui punct material de pe axele de coordonate (si am obtinut rezultatele cunoscute la școală). Merită? Da, este, în primul rând, pentru că am înregistrat legile mișcării în invariantul. cum se spune, forma care nu depinde de alegerea unui anumit sistem de coordonate. În al doilea rând, am înregistrat relații sunt valabile în cazul mai general, atunci când luăm în considerare rotirea unui sistem sau a unui corp solid ca întreg (fig. 8).
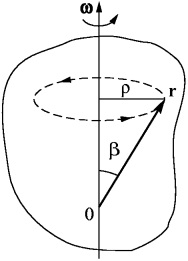
Fig. 8. Rotație a solidului.
Având în vedere această imagine, este ușor de a arăta că aici, chiar dacă # 969; și r nu sunt perpendiculare una pe cealaltă, cu toate acestea, fostul raport este efectuată pentru o anumită viteză a punctului ales cu vectorul raza r.
Într-adevăr, așa cum se arată în Fig. 8. un punct de-a lungul unui cerc se deplasează cu o rază # 961; = Sin R # 946; cu viteza # 965; = # 969; # 961; = # 969; r păcat # 946;. ci ca # 946; - este unghiul dintre vectorii # 969; și r. vom vedea validitatea acestei formule.
Acum înțelegem originea unui termen suplimentar în accelerația centripetă (a se vedea figura 9 ..):
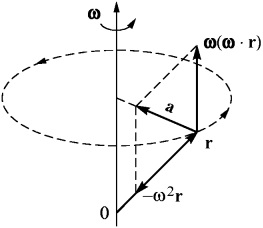
Fig. 9. accelerație centripetă.
Astfel, accelerația a nu este de fapt îndreptat spre centrul și vpascheniya axa, așa că ar putea fi numit osestremitelnym. Dar pazumeetsya, nu este în titlu.
În favoarea relația v = [# 969; r ×] este faptul că deține, în cazul mai general în care vectorul viteză unghiulară # 969; Nu este constantă și depinde de timpul: # 969; (T). Apoi, cu formula de schimbare de accelerare - un termen suplimentar apare în ea:
valoare # 946; = D # 969; / Dt se numește accelerația unghiulară. Se pare că atunci când schimbarea vitezei unghiulare (încetinind, de exemplu, o rotație în jurul unei axe fixe) sau rotit cu rotirea axei în sine în timp (sau ambele).
Fig. 10. Poziția relativă a vectorilor de unități.
In concluzie, pentru referință pentru a da un vector de expresie componente carteziene prizvedeniya C = [A x B].