Sub linia de orientare pe sol (hartă) se înțelege poziția sa în raport cu direcția nord sau axa X. meridianul Poziția determinată de unghiul dintre direcția nord și direcția acestei linii. Deoarece unghiurile care determină direcția liniilor sunt azimutul și azimutul rumba. Liniile de intrare pentru orientare în geodezie adoptate: true (geografic) meridianul axial zona meridian și meridianul magnetic. zona liniei de orientare a adevăratei meridianului este realizat de unghi, numit adevăratul azimutul.
Adevărații zone de linie de azimut la un anumit punct este numit un unghi orizontal între direcția adevăratei meridian nord la acel punct și direcția liniei. Acest unghi este măsurat în sens orar de la direcția meridianului de Nord. Adevărata azimutul notată cu litera A și variază 00-3600.
Azimut linie direcția înainte (R1R2), se numește azimut directă și inversă direcției - azimut înapoi. (. Figura 28) azimut Direct R1R2 este A1, iar revenirea la aceeași direcție - A2. Deoarece meridianele nu sunt paralele între ele și se intersectează la polul (Pn), azimutul liniei la fiecare punct are o valoare diferită. Unghiul dintre cele două direcții ale meridiane din cele două puncte (P1 și P2), se numește convergență (g) meridiane. După cum se poate observa din Fig. 28, relația dintre forward și reverse azimuturilor pot fi scrise 28 formula.
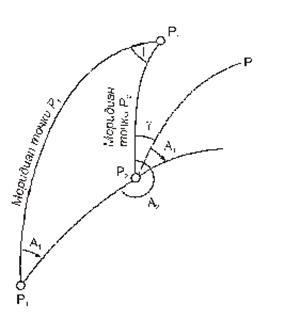
unghiurilor de azimut ca viza inapoi aplicabile pentru sferoidală sau suprafața sferică a Pământului. În cazul în care planul imaginii la suprafața pământului, de exemplu, în proiecția Gauss-Kruger, sunt unghiul de viza inapoi plan, numit unghi de direcție.
Unghiul direcțional al liniei pe planul este unghiul dintre direcția nord sau meridianul axial și direcția axei X (R1R2), la un anumit punct (Fig. 29). Unghiurile direcționale, notate cu litera A ca azimuturilor măsurată ca variază de la 0 ° la 360 °.
După cum se poate observa din Fig.29, telecomunicații între liniile direcționale unghi și azimut exprimat prin formula 29:
aici g - convergența meridiane la punctul P1. Convergența meridiane este măsurat de la meridianul adevărat la meridianul axial.
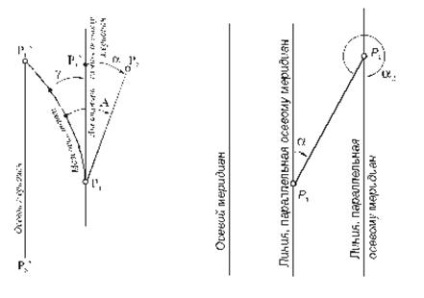
Unghiurile înainte și invers direcționale ale aceleiași linii diferă prin 1800 (Fig. 30).
Convergența meridiane se calculează cu formula aproximativă:
unde # 966; cp - latitudine geodezică în mijlocul liniei R1R2; egal cu (# 966; P1 + # 966; p2) / 2); # 916; # 955; - diferența de puncte longitudine P1 și P2.
Apropierea de puncte meridianul situat la est de primul meridian are semnul plus, și la vest - minus.
lagăre magnetice. La rezolvarea o serie de probleme practice, este recomandabil să se folosească lagăre magnetice, deoarece acestea sunt ușor determinate cu ajutorul unor dispozitive simple, cum ar fi o busolă și o busolă, care este principala parte a acului magnetic.
Este cunoscut faptul că sub influența magnetism terestru ac magnetic suspendat liber este instalat în planul meridian magnetic al punctului. Unghiul pe care îl formează cu planul meridian geografic se numește declinație magnetică este notat cu d (Fig.31).
Este măsurată de declinația direcția nord adevărat meridianul (C), la est este pozitiv ( „Est“); la vest - negativ ( „Vest“).
polii magnetici ai Pamantului nu coincid cu adevărat, astfel încât există un declin. Linia de legătură polilor magnetici ai Pământului de axa de rotație a Pământului cu un unghi care este de 11 °, 5 și nu trece prin centrul său.
lagăre magnetice (AM) și contorizate ca fiind adevărate - în sens orar 00-3600, dar direcția de meridianul magnetic.
Poziția linie pe hartă sau pe sol a determinat încă concepte, cum ar fi cvadrantul.
Rumb - este un unghi ascuțit măsurat de cele mai apropiate direcții meridian (nord sau sud) direcția spre linia (fig. 32).
Rumb variază de 0-90 și un nume (un sfert în care se află linia).
Relația dintre rumba și azimutului este dată în tabelul 3.
Relația dintre azimutul magnetic și azimutul adevărat cu semnul declinare este după cum urmează:
Sub granița de sud harta topografică indică valorile medii ale declinația acului magnetic și convergența meridiane (cu semnele lor).
Legătura dintre unghiul direcțional și azimutul magnetic este determinat prin rezolvarea celor două ecuații (formule 29 și 31), în care laturile de stânga sunt egale, și, prin urmare, vor fi egale și dreapta
unde găsim o = Am + # 948; - # 947; (32)
(G și d În ea sunt cantități algebrice.).