Planar grafic - un grafic care este desenată pe planul astfel încât două dintre marginile sale să nu se suprapună.
grafic planar - un grafic izomorf la un grafic plan.
Figura A) - plane, dar nu plat, graficul b) un grafic planar.
Fiecare grafic plan împarte planul pe marginea: interior - și exterior limitat - nelimitat.
Studiul graficelor planare a fost inițiată de Euler, în studiul său de poliedre. Formula Urmatoarea lui Euler - este un rezultat clasic în matematică, în cazul în care - numărul de noduri - numărul de muchii - numărul de fețe ale poliedru. Formula lui Euler este valabilă în cazul mai general al unui card de plată - conectat grafic planar, luate împreună cu toate aspectele sale.
Teorema. Lăsați un card de avion are vârfuri, muchii și fețe. Apoi, avem următoarea ecuație:
Dovada. Noi folosim inducție după numărul de muchii.
Dacă, atunci formula (1) se prezintă sub forma următoare :.
Să presupunem că nu mai formula (1) este valabil pentru toate cardurile cu un număr de aripioare plane. card de plată, cu numărul de muchii obținute de la un card de plată cu numărul de muchii în două moduri:
1) adăugarea de noi noduri, muchie care leagă unul dintre nodurile vechi;
2) compusul nu este o muchie a două vârfuri adiacente.
În primul caz, formula (1), se verifică după cum urmează:
.
În al doilea caz, o nouă față și cu formula (1), se verifică după cum urmează:
.
Corolar 1. Dacă în format de card de fiecare față de nodurile inel,
Dovada. Numărul de muchii care aparțin fiecare parte a acestuia. Deci, numărul de noduri care urmează să fie numărate la fiecare față, de asemenea. În acest caz, fiecare muchie este numărată de două ori, astfel încât numărul de noduri este recalculat. Obținem egalitate. Substituind în (1) și găsiți (2).
Teorema Kuratowski. Grafic este plană, dacă și numai dacă nu conține un homeomorf subgrafic sau.
35. Graficul complet. Count K4 și K5 grafic planar nu este planar.
Graficul maxim plan este un grafic plan care adăugarea de orice margine încetează să mai fie plană.
Din definiția rezultă că graficul maxim planar toate fețele sunt triunghiuri (fațete cu trei vârfuri):
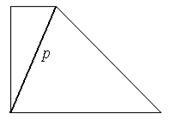
dacă linia conține un dreptunghi (sau un poligon cu mai multe laturi), este posibil să se adauge un avantaj care nu schimbă planeitatea graficului, dar lipsindu proprietățile graficului să fie grafice ca planare.
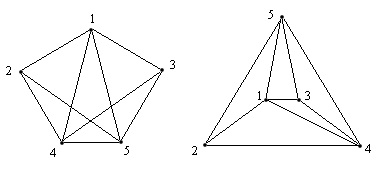
Exemplu. În următorul grafic, puteți adăuga doar o singură margine, după care acest grafic este tras în grafic.
Lema. Dacă - și planare-grafic, atunci
.
Dovada. Cel mai mare număr de muchii într-un grafic planar are un grafic cu toate fețele - triunghiuri. Maximal planar Graficul toate fațetele - triunghiuri. Substituind în (2). Obținem.
Teorema. Graficele nu sunt plane.
Dovada. În cazul în care (5.10) plane -graph, atunci lema nu este îndeplinită :.
36. graf bipartit. Count K2,3 și K3,3 grafic planar nu este planar.
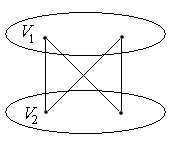
Un grafic se numește bipartit-grafic. dacă setul de vârfuri este format din două porțiuni non-gol (,) în interiorul căruia nu există margini.
În cazul în care toate nodurile sunt conectate cu toate nodurile, atunci graficul este numit graf bipartit complet, și este notată cu.
Aici este graficul complet bipartit cu numărul de noduri nu este mai mare de 4:
Maximum graf bipartit planar numit graf bipartit plan care adăugarea de orice margine încetează să mai fie grafic planarnymdvudolnym.
Dacă - graficul maxim planar bipartit, fiecare dintre fața ei este un patrulater:
Exemplu. În următorul grafic, puteți adăuga doar o singură margine, după care graficul se referă la grafic:
Lema. Dacă - planar graf bipartit, apoi -graph
.
Dovada. Cel mai mare număr de muchii într-un grafic bipartit are un grafic planar cu toate fețele - quad-uri. Maximal planar Graficul toate fațetele - quad-uri. Substituind în (2). Obținem.
Teorema. Graficele și nu plane.
Dovada. În cazul în care (6.9) planar -graph, atunci lema nu este îndeplinită :.