Pentru a afla ce determină natura rotației corpului în jurul unei axe fixe, luați în considerare următorul experiment. Luați corpul în formă de cruce de lumină, capetele cărora sunt fixate sarcini masive egale m (fig. 87).
În centrul crucii se va consolida scripetele în trepte. Crossbar împreună cu roata de transmisie a pus pe punte, având grijă ca frecarea când se rotește în jurul axei care a fost neglijabil.
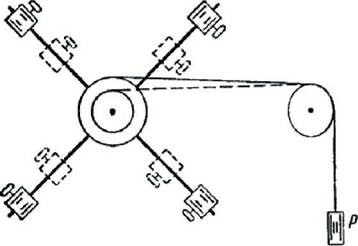
Atașați la una dintre etapele de capătul fulie firului, înfășurați în jurul scripetelui și, prin aducerea capătul liber al firului prin blocul, suspendarea acestuia P. La eliberarea încărcăturii de marfă P. va trece în rotație cu creșterea vitezei unghiulare # 969;, iar rotația va fi accelerată în mod uniform.
Varierea sarcină P, raza fulie l, m masa mărfurilor și distanța R lor față de axa de rotație a „explora modul în care acești factori afectează valoarea accelerației unghiulare. Rezultatele acestui studiu sunt reduse la faptul că accelerația unghiulară
1) direct proporțional cu tensiunea firelor raza fulie L și L;
2) este invers proporțională cu masa m a mărfurilor și pătratul R lor distanța față de axa de rotație.
În consecință, accelerația mișcării de rotație nu depinde numai de mărimea forței f care acționează asupra corpului, dar, de asemenea, pe distanța l de axa de rotație la litiu, de-a lungul căreia acționează forță. Produsul dă fl valoarea așa-numitul moment de forță în jurul axei de rotație.
Din experiența ar trebui să fie, de asemenea, luate în considerare faptul că valoarea accelerației unghiulare afectează nu numai masa corpului rotativ, dar distribuția greutății în jurul axei de rotație. Dimensiune, luând în considerare atât aceste circumstanțe, este cunoscut sub numele de momentul de inerție față de axa de rotație.
Astfel, pentru a studia mișcarea de rotație necesară introducerea a două noi cantități fizice - cuplul și momentul de inerție.
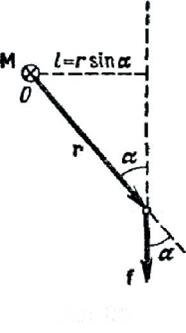
Să începem cu o explicație a conceptului de moment de forță. Momentul de inerție vor fi discutate în paragrafele următoare. Momentul unei forțe cu privire la un punct. Momentul forței f în raport cu un punct G este o cantitate vector M, definit prin expresia
Acum imaginați-vector forță f ca sumă a trei componente: f || -parallel axa z, fR-coliniari vector R și în final fx - perpendicular pe planul care trece prin axa z și R. vectorul în Fig. 94, această componentă este prezentată printr-un cerc cu kre-
Momentul total al forțelor interne. Forțele care interacționează unele cu altele, oricare două mase elementare se află pe aceeași linie (fig. 95).
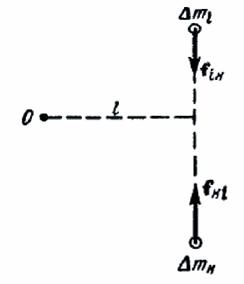
momentele lor cu privire la orice punct O, sunt egale în mărime și opusă în direcția. forțe echilibru De aceea momentele interne reciproc în perechi, iar suma momentelor tuturor forțelor interne ale sistemului pentru orice puncte de material, în special solid, este întotdeauna zero. Acest lucru este valabil și pentru c ummarnogo moment al tuturor forțelor interne, luate cu privire la orice punct „și pentru moment totală a forțelor“, luate în jurul oricărei axe.
[1] Ulterior, vectorii sunt perpendiculare pe planul figurii, vom descrie un cerc cu o cruce, dacă vectorul este direcționat de la noi, și un cerc cu un punct în centrul său, în cazul în care vectorul este îndreptată spre noi. Pentru claritate, ne putem imagina un vector în formă de săgeți, cu un vârf conic și Phillips penajul coadă Apoi, în cazul în care vectorul este direcționat la noi (săgeata zboară la noi), vom vedea un cerc cu un punct, în cazul în care vectorul este direcționat de la noi (o săgeată zboară de la noi) vom vedea un cerc cu o cruce.
[2] Componenta Mz trebuie să fie distinsă de proiecția vectorului M în axa z. notat cu simbolul vectorului MzMz, Mz - valoarea algebrică scalară; între noi există o relație simplă: Mz = ezMz în cazul în care ez. - vectorul unitate (versorul) axa z [simbolurile denotă vectorul unității k vezi ecuația (28).]