Se spune că arta de a geometriei pentru a construi o dovadă corectă pentru desenele greșite.

Pe această tabletă de lut veche reprezintă rădăcina pătrată a doua, calculată până la trei caractere în sistemul șaizecelea, care a fost folosit de babilonieni, in jurul anului 1700 î.Hr.. Fotografie de Bill Casselman
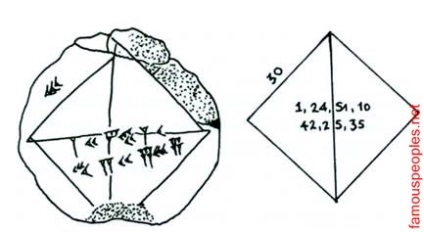
Numerele cuneiforme babiloniene pe laturile și diagonalelor pătrat (pe partea stângă) corespund modern (dreapta) pentru un pătrat cu latura de 30, care este calculată pe diagonală. Două numere scrise (în sistemul șaizecelea de calcul) da: primul - 1.414212963, o bună aproximare pentru rădăcina pătrată a 2; al doilea - 30 x 1.414212963 produs, lungime diagonală, calculată în conformitate cu teorema lui Pitagora
Euclid a sintetizat ideile marilor matematicieni ai pitagoreici, cum ar fi Archytas, precum și activitatea lui Hipocrate, Eudoxus și Theaitetos, se adaugă cu propriile lor gânduri și combinate într-o secvență logică numită „elemente“. Această lucrare este compusă din 13 cărți scurte, el a devenit cel mai faimos manual din istoria omenirii. Este o mare comoară de argumente matematice fine care demonstrează puterea metodei axiomatice în acțiune. Euclid a luat ca bază axiomele net, sau trimiterea, și de a folosi sistematic reguli logice de raționament construit teorem28 dovezi. Această tehnică este deducere meticuloasă a devenit un model pentru oamenii de știință din diferite domenii de mai multe milenii. De la Fomy Akvinskogo la Spinoza vom vedea metoda de raționament, care reflectă structura dovezilor lui Euclid. Dezvoltarea gândirii filosofice este indisolubil legată de noțiunile de filosofi și teologi despre matematică, pe care le considerau ca parte a esenței absolute a lucrurilor, mai degrabă decât doar o descriere sau model al realității.
Până la începutul secolului al XIX-lea se credea că geometria euclidiană descrie spațiul real real. Când Riemann, Lobacevskil, Bolyai și Gauss a formulat geometria non-euclidiană care descriu structura suprafețelor neliniare, cum ar fi o sferă sau o șa este scuturată filozofie la miez. geometria euclidiană a devenit brusc doar una din multele: complete și consistente logic, având în vedere propriul lor set de axiome irefutabile. Astfel, descoperirile geometrice au contribuit la dezvoltarea gândirii relativist. Adevărul absolut a fost respinsă în geometria precum și în politică, religie și cultură.
Nu există nici o dispută, amploarea și profunzimea impactului pe care a produs cărțile Euclid, este fără precedent. Dar există un singur subiect, urmat de o imagine cunoscută în învățăturile sale, care a devenit cunoscut tuturor celorlalți. Aceasta este ultima dintre cele 48 de teoreme în prima carte a „elemente“: proprietatea, comune tuturor triunghiurile in unghi drept si familiar pentru noi sub numele de Pifagora29 teorema. Ia orice triunghi cu laturile A, B și C, unde C - cea mai lungă latură (ipotenuza), atunci A2 = B2 + C2.
O legenda spune ca Pitagora (aproximativ 580-500 î.Hr.) a descoperit această teoremă în palatul lui Polycrates, conducătorul tiran al insulei Samos. Se așteaptă până când a fost admis la conducătorul, Pitagora a studiat tiparele pe podeaua camerei exterioare a palatului. A fost un mozaic de pătrate. El a observat că, dacă trage o linie diagonală care împarte pătrat în două triunghi dreptunghic, aria pătrat construit pe diagonală va fi egală cu cele două pătrate ale pătrat, construit pe partea. Cu alte cuvinte, pătratul ipotenuzei este egal cu suma pătratelor celorlalte două laturi ale triunghiului. Acesta este un caz în care, în formula de mai sus A = B. Ei bine, o poveste interesantă!
„Elemente“ teorema lui Euclid arată o situație mai generală, atunci când A nu este neapărat egal cu B, cu referire la desen, care este Capul de linie oarecum similare pe care un scaun nevesty30 filmate nunta. Teorema afirmă că aria pătratului este egală cu suma suprafețelor BCED pătrate Hanks și GABF.
De fapt, există sute de diferite dovezi ale teorema lui Pitagora, și știm că acesta era cunoscut la babilonieni, chinezi, indieni și egipteni cu mult înainte de nașterea lui Pitagora. Babilonienii a știut cum să construiască un triunghi cu A, B și C, corespunzând raportului lui Pitagora, chiar înainte de 1600 î.Hr..
Pe un mic tablete cuneiforme Fotografia este plasat la începutul acestui capitol prezintă un pătrat și diagonală. Înscrisă pe ea semne cuneiforme înseamnă lungimile laturilor în sistemul de numărare sexagesimal mixt zecimal, care a fost folosit de către babilonieni. parte a pătrat este egală cu 3 x 10 = 30; știind teorema lui Pitagora, presupui că lungimea diagonalei este de 30 x V2, adică raportul dintre diagonalele egal cu rădăcina pătrată a 2. Aici, în sistemul sexagesimal (în care multiplicarea cu 30 ca o diviziune de 2), lungimea diagonalei este înregistrată 42; 25,35 și 1; 24,51,10 este egal cu rădăcina pătrată a 2. Dacă transferul șaizecelea înregistrare în zecimal, se dovedește că valoarea Babilonului este: 1 + 24/60 + (51/60 2) + ( 10/60 3) = 1.41421296, care este o aproximare excelenta, cu cea mai mare precizie la șase zecimale (patru cifre sexagesimale).

Teorema lui Pitagora într-una dintre primele exemplare grecești ale „elemente“ ale lui Euclid
Cele mai vechi dovezi cunoscute de teorema lui Pitagora este într-un anumit sens unic și frumos. Acesta poate fi găsit în cele mai vechi existente chineze matematice tratate - „calcul Canon Chou gnomon“, dintre care unele părți datează la aproximativ 600 m-BC. Trebuie să desenați patru triunghi rectangular identic cu laturile A, B și C într-un pătrat mare. Apoi, devine evident că o mare suprafață a pătrat (A + B) 2 = A2 + B2 + 2AV egală cu suma suprafețelor de patru triunghiuri, adică 4 x 1 / 2AV plus un mic pătrat zonă C2 centrală. Rezultă că A2 = B2 + C2. Sau chiar mai ușor - muta patru triunghiuri în piața mare, astfel încât să formeze două dreptunghiuri.
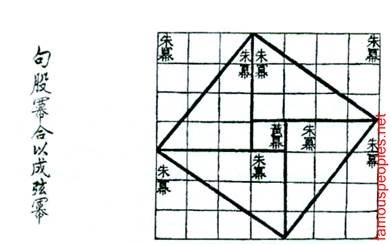
dovada grafică chineză a teorema lui Pitagora 600 BC: o mare suprafață a pătrat este egală cu suma suprafețelor de patru triunghiuri unghi drept și un mic pătrat în interior
Veți vedea că zona din interiorul pătratului, care nu sunt acoperite de triunghiuri în ambele imagini vor fi aceleași, deci, A2 + B2 - C2.
Am putea adăuga că desenele incorect desenate pot fi o sursă de erori grave. În Evul Mediu a existat conceptul de falsigrafiya, care este greșit construit desene și dovezi. Procesul laborios de copiere a manuscriselor vechi manual de multe ori a condus la faptul că cifra a trecut sau copiat mai degrabă neglijent. Din aceleași motive, uneori se dovedesc a trecut și desenele selectate doar furnizate pentru a ilustra soluții teoremă. Există, de asemenea, exemple în care cifrele sunt prezente, dar care nu sunt însoțite de explicații cu privire la cartea de probleme care pot fi puse întrebări care trebuie să se răspundă. Poate că este ceva de genul un pat de copil, cum ar fi cele folosite pentru a se pregăti pentru examene? Sau materiale didactice cu lacune, care au trebuit să umple elevii medievale?
Diagrame și desene în acest capitol - nu este pur și simplu o reflectare a lunga istorie a celebra teorema. Ei, și mulți alții ca ei, au făcut obiectul unor dezbateri aprinse. In 1934, o companie mica de matematicieni francezi, a cărui suflet a fost André Weil, folosit pentru a aduna într-o cafenea „Kapulad“ în Cartierul Latin din Paris. Ei au stabilit să reformuleze diferitele ramuri ale matematicii în noua formă strictă de realizare intrinsecă pentru toate structura logică.
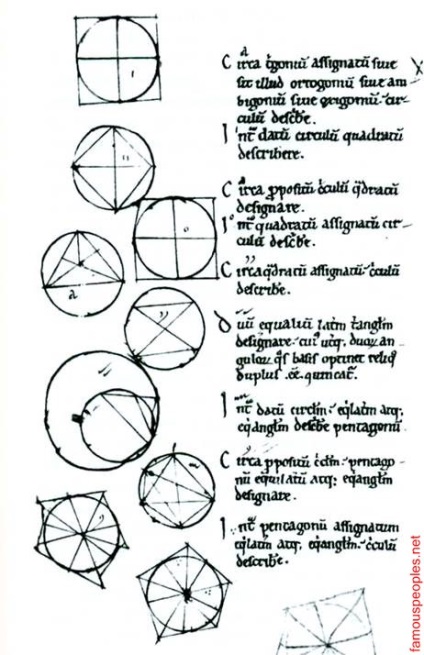
A patra carte a lui Euclid, o copie scrisă de mână a secolului al XII-lea în limba latină. Aici am stat teoreme fără dovezi și sunt desene incomplete, astfel încât studenții să poată folosi pentru a le eticheta și pentru a finaliza dovada. Adelard original compilat din Bath, în care se face copia, conținea nici o dovadă. Rețineți că fiecare imagine conține note sau semne care indică cititorului, la care se referă declarația. De exemplu, un cerc mare cu un cerc mic în interior (a patra de jos) este marcat de două căpușe, care se conecteaza cu aprobarea al șaselea pe listă, care este marcat cu litera d
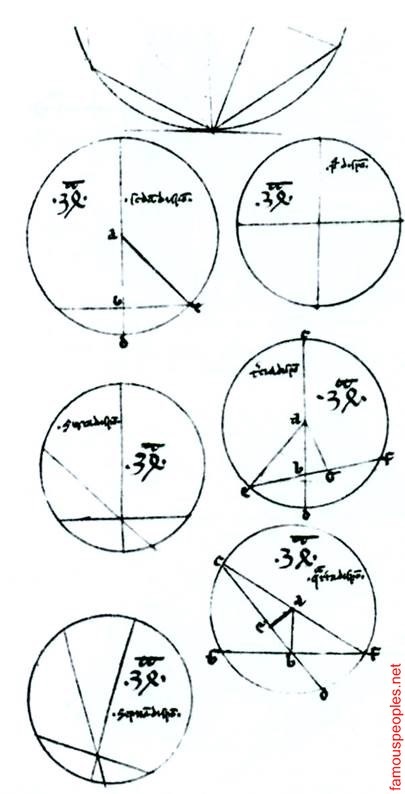
Un fragment dintr-un manuscris din secolul al XIV-lea, în care declarațiile omise și dovezi ale teoremele lui Euclid, dar a salvat desenele însoțitoare, astfel încât cititorii pot veni cu dovada de propria lor. Acesta prezintă diverse cazuri de Teorema 3.4 Cartea a III, care prevede că, pentru orice coardă, care intersectează segmente de cerc ale unuia dintre acordurile formează un dreptunghi a cărui suprafață este egală cu aria dreptunghiului definit de segmentele de-a doua coardă. Diferitele figuri ilustrează diferite cazuri de aranjament de acorduri

În primul rând knizhka- „clapetă“ a fost dedicat geometria tridimensională. Prima traducere a lui Euclid în limba engleză, publicată la Londra în 1570 sub titlul „Elemente de geometrie a Filozoful antic Euclid Megara, cum ar fi (prima dată) Tradus în limba engleză de către Henry Billingsleem“ au fost folosite ingenios volumetrica desfășurare ilustrare.
Bourbaki texte de membri ai cercului au fost dezvoltate în cursul discuții și critici nemilos. Ei au apărut pentru prima dată fragmente diferite de notație matematice moderne și de terminologie, iar acum foarte puțini oameni dau seama că îi datorăm existența lor Bourbaki. Cu toate acestea, activitatea Bourbaki a făcut impactul pe care mulți matematicieni, în special aplicarea, considerate distructive. El sa bazat pe structura matematică în detrimentul problemelor și exemple. Ei nu au avut desene. intuiție matematică a fost, părea închisă într-o cămașă de forță axiomatică. Accentul pus pe structuri comune într-o varietate de cercetare matematică a devenit în cele din urmă afectează programa școlară în multe țări, dând naștere la așa-numita noua filozofie a matematicii. Evoluțiile au arătat că această tehnică nu a reușit. Ea a explicat concepte dificile prea devreme, în plus, fără a rezolva problemele din copiii de școală a fost dificil să se dezvolte abilitățile matematice și pentru a genera motivația necesară. Este la fel de important ca noua metodă nu a permis părinților să ajute copiii lor, deoarece ei pur și simplu nu au fost familiarizați cu „noua matematica.“
grupul Bourbaki a dorit să elimine practica probelor în desen, în cazul în care rolul principal jucat în schema de raționament matematic.
Această filozofie nu a fost cu totul nou. Binecunoscutele patru volume „Mecanică analitică“ Lagrange (1788), caracterizat printr-o lipsă totală de desene geometrice și idei.
Marele predecesorul Lagrange, Isaac Newton a folosit desenele ori de câte ori au fost utile, așa cum suntem acum. La urma urmei, știm că, dacă este posibil dovada a desenului, există o modalitate de a formaliza și logică și se aplică soluția la o gamă largă de exemple nu este în mod necesar acoperit de model nu este întotdeauna clar pentru ochi aceste mintea lui. Euclid, de exemplu, a căutat să rezume teorema lui Pitagora originală, înlocuind pătratele de pe celelalte laturi ale unui triunghi dreptunghic forme.
Până în 1980, după ce membrii de bază ai cercului Bourbaki retras și sa încheiat procesul lent cu editorii, acesta a scăzut. Mai mult de 20 de ani au trecut fără nicio echipă de publicații notabile, iar influența sa diminuat. Poate că suntem pur și simplu prea imagini de dragoste? Dar această concluzie este, probabil, prea ușor să locuiască pe ea. Bourbaki și respingerea mulți matematicieni au arătat că matematica are două culturi. Ei sunt cei care preferă să construiască structura și formalizarea unui grad ridicat de generalitate, iar cei cărora le place să pozeze și de a rezolva probleme specifice (deși nici un matematician nu poate fi atribuită în mod exclusiv la una dintre aceste tabere). Ea poate domina uneori metodele abstracte, și vice-versa. Această diferență de opinie cu privire la care a tendințelor este (sau ar trebui să fie) dominant, probabil, poate fi considerat un semn, bun, care arată că există încă un echilibru sănătos între cele două.
Legate de posturi:
«Stele anterioare și noapte înstelată. Whirlpool Galaxy Next „Razboiul Lumilor. Canal marțian