Un credit de 63 TR eliberat timp de 4 ani. Cu o rată a inflației de așteptat de rata reală de 14% a rentabilității operațiunii ar trebui să fie de 9% a ratei dobânzii complexe. Se determină rata dobânzii la împrumut, ținând cont de inflație, suma de rambursare și dobânda acumulată.
1) Prima parte a problemei se va rezolva în două moduri:
a) Calculul pariurilor va produce formula I. Fisher:
Prin urmare, pentru a compensa pierderile datorate inflației și pentru a asigura profitabilitatea la nivelul de 9% pa (interes compus) trebuie instalat rată nominală egală cu 24.26% brut.
b) Calcularea ratei procentuale estimate pe baza formulei:
Timp de un an, m = 1 și n = 1.
De aceea, înlocuind în formula 2 valorile m și n obținem:
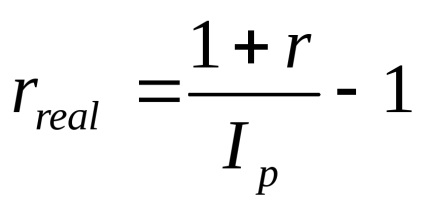
2) se calculează suma calculată prin formula:
Ajustate la inflație, banca va primi:
Dintre acestea, valoarea de rambursare a datoriei va fi:
Astfel, numai din cauza datoriei inflației a crescut cu:
106,404.49 - 63,000 = 43,404.49 ruble.
Dobânda acumulată, ajustat pentru inflație va fi:
150,198.62 - 63,000 = 87,198.62 ruble.
În realitate, banca va primi venituri numai în sumă de:
150,198.62 - 106,404.49 = 43,794.13 ruble.
Răspuns: inflație:
rata va fi de 24.26%;
valoarea datoriei rambursată 106,404.49 ruble.;
dobânda acumulată (venitul băncii) va fi: 43,794.13 ruble.
Acesta a acordat un împrumut în valoare de 18,0 mii. Frecați. pentru o perioadă de 6 luni la 24% pe an, cu rambursare lunară. Rambursarea se face in rate lunare. Fii planul de rambursare a creditului cu plata uniformă a principalului.
Declarația problemă nu este specificat tipul de împrumut și metoda de încărcare a dobânzii. În acest caz, creditorul va fi mai profitabil să emită un credit „Credit de consum“ (dobândă simplă), deoarece termen lung a creditului mai puțin de un an.
1) Să presupunem că calculul dobânzii efectuate pe datoria rămasă.
Valoarea plății extinctive este format din două părți:
A) Plata principalului (el este o constantă, cu condiția, că este de 18.000 de ruble. / 6 luni. = 3000 ruble).
B) rambursarea de plată a dobânzii acumulate (în acest caz, am presupus că se percepe dobândă la soldul datoriei). Prin urmare, valoarea dobânzii acumulate la maturitate va fi egală cu:
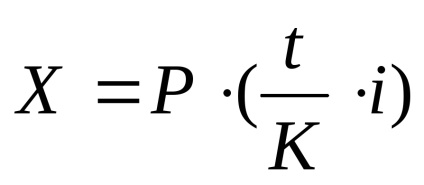
unde
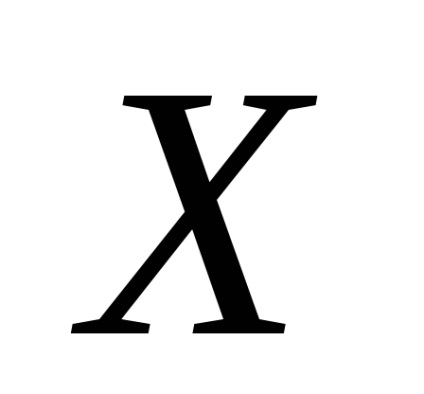
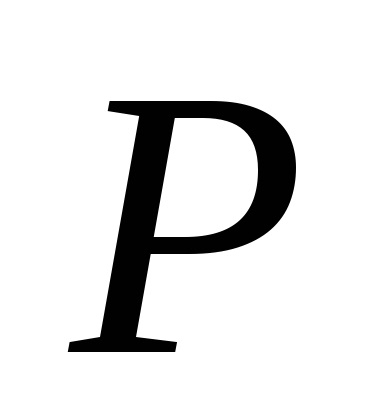
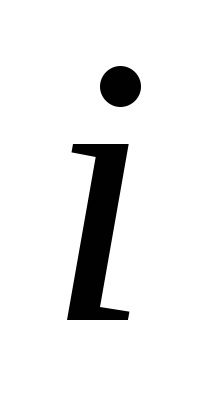
t - numărul de zile ale operațiunii (în acest caz de 30 de zile);
K - baza de timp (360 de zile).
Pentru prima plată a dobânzilor acumulate va fi: freca.
Pentru a doua dobânda de plată acumulată va fi: freca.
Suma dobânda acumulată pentru a treia plată: freca.
Suma dobânda acumulată pentru a patra: freca.
Pentru a cincea dobânda de plată acumulată va fi: freca.
Suma dobânda acumulată pentru a șasea tranșe: freca.
Planul de plată este după cum urmează:
2) Să presupunem că dobânda acumulată pe întreaga datorie dintr-o dată, atunci logica de creditare creditor va încerca ca venitul lor (dobânda acumulată), și, prin urmare, fluxul de plăți pentru a achita dobânda acumulată, cât mai curând posibil pentru a elimina uniform descrescătoare. Pentru elaborarea unui astfel de plan de plăți extinctive mai rezonabil să se utilizeze „Regula 78“, cu toate că puteți utiliza orice secvență descrescătoare a fracțiunilor, atâta timp cât suma lor este egală cu 1.
La început se calculează fracțiunile:
A) Nr luni sumă va fi de 0,5 ani:
B) Fracțiunile sunt după cum urmează:
Pentru prima plată:
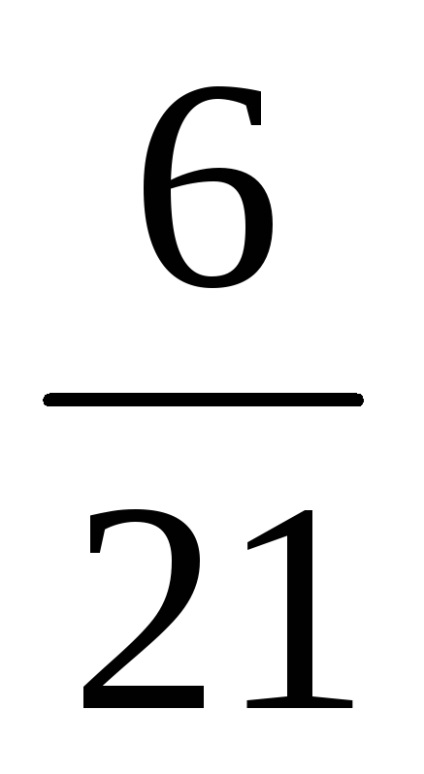
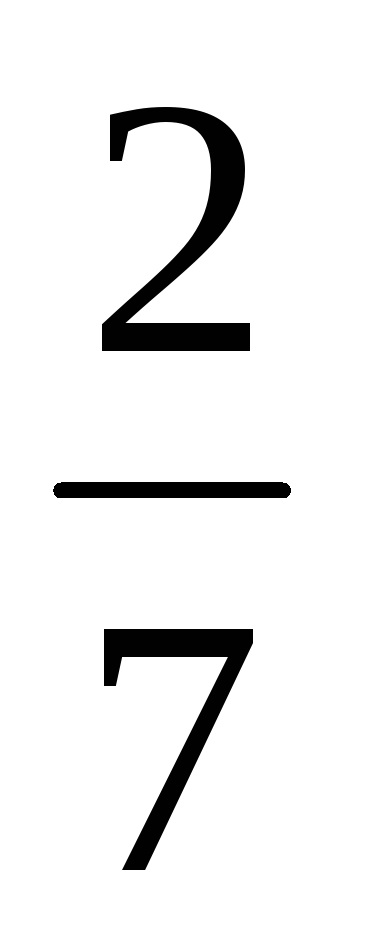
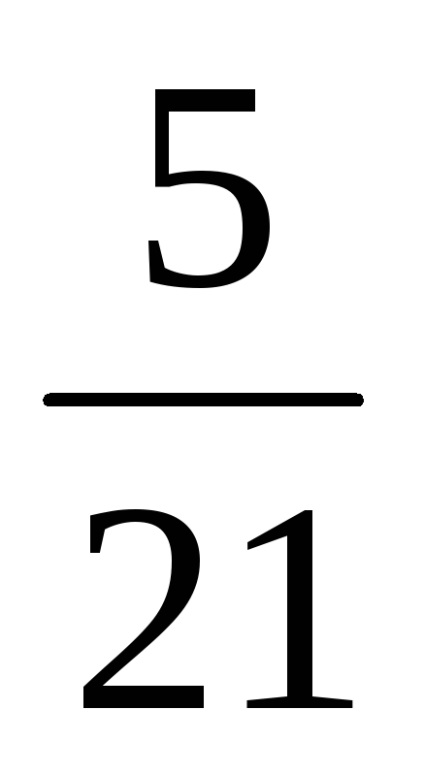
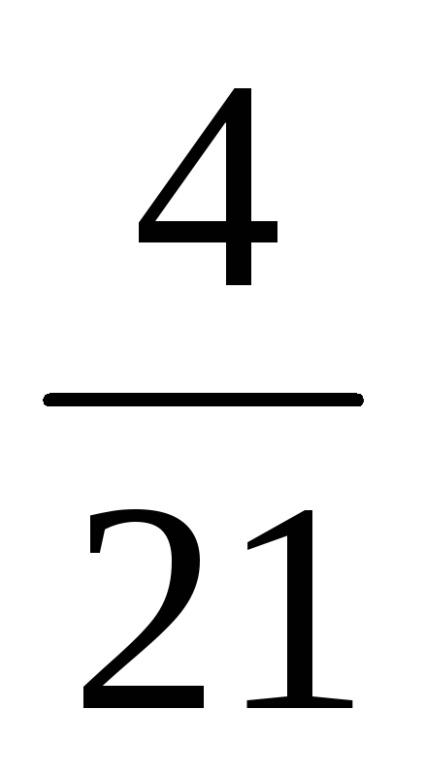
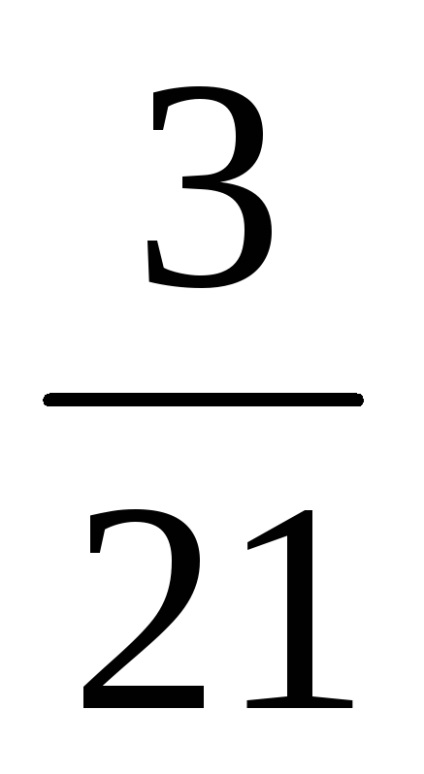
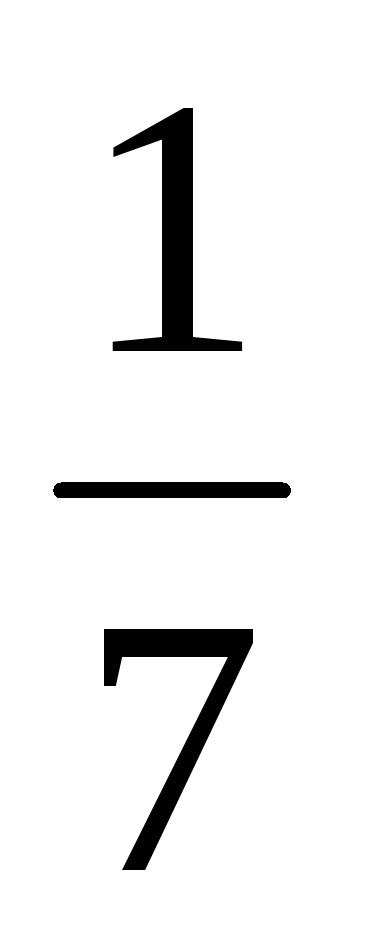
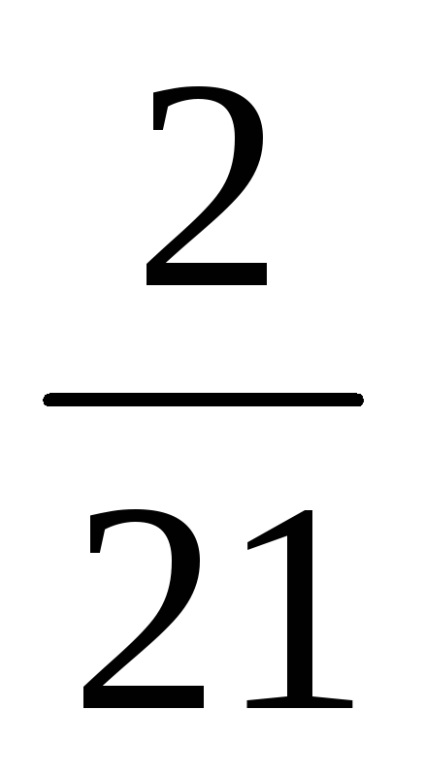
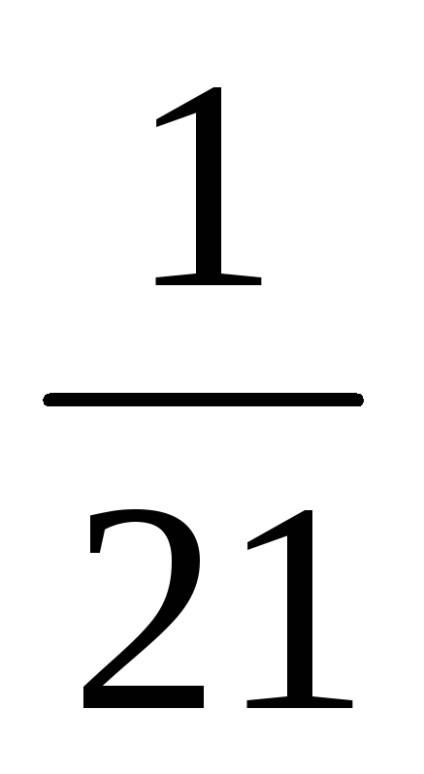
Calculăm valoarea dobânzii acumulate:
Acum, înmulțiți valoarea dobânzii acumulate în fracțiunea plăților respective, vor primi suma de rambursare de interes.
Sold la data de începere
Valoarea plății principalului
Reziduul la sfârșitul perioadei de
Banca la acordarea de credite timp de 1 an 6 luni, a folosit o rată de 25% pe an, dobânda se plătește la fiecare șase luni. Se determină valoarea unei rate a dobânzii simple, care ar oferi banca pentru a obține o sumă echivalentă.
Suma rambleu va fi egală cu:
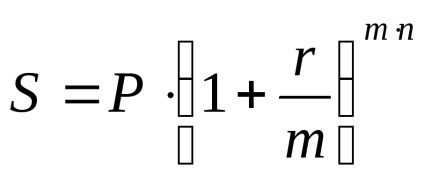
Suma rambleu pentru o rată de actualizare simplu va fi egală cu:
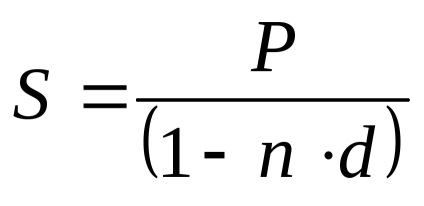
Împrumut în valoare de 1 mln. Frecați. cu interes anual la rata de 20% pe an se rambursează în termen fix egal de plătit, inclusiv rambursarea principalului creditului și a dobânzilor anual, la sfârșitul fiecărui an, timp de 5 ani. Se determină costul total de rambursare a creditului și dobânda acumulată.
De fapt, considerăm două versiuni de plată:
A) o singură dată rambursarea principalului și a dobânzii acumulate timp de 5 ani:
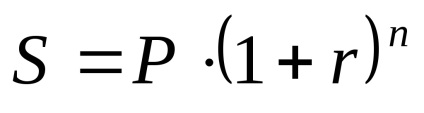
Astfel, dacă am stins împrumut într-o singură plată după 5 ani, ar plăti 2,488,320.00 ruble.
B) Cu toate acestea, suntem invitați să stingă datoria în rate egale, la sfârșitul anului. Apoi, din formula pentru determinarea valorii unei anuități ordinare atrasă (postnumerando) că valoarea plății va fi egală cu:
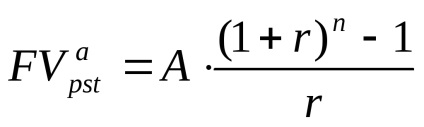
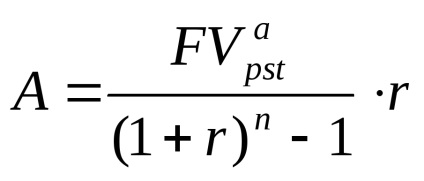
Astfel, plățile egale anuale se ridică la 334,379.70 de ruble.
În consecință, costul total ar fi: 334,379.70 ruble. × 5 = 1671898.50 RUB. Dintre acestea, interesul: 1,671,898.50 ruble. - 1000000 ruble. = 671,898.50 ruble.
Pentru o reprezentare mai vizuală a costului total de rambursare a creditului și dobânda acumulată de carte de depozit este metoda se aplică: