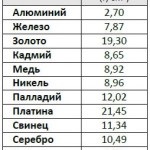
Niciodată nu obosește să repete, că masa corpului - este volumul înmulțit cu densitatea materialului (a se vedea tabelul densităților.):
Cu toate acestea, în cazul unei părți gol sau gol la interior, nu vom avea de a face cu volumul de corpul ei, precum și cu volumul zidurilor sale. ziduri de deplasare ale elementului tubular este reprezentat cel mai ușor ca diferența dintre cele două volume ale corpurilor solide: dimensiuni externe și interne (ale volumului corp complet al volumului golurilor interioare se scade).
Formula pentru volumul corpurilor solide pot fi găsite în articolul „Masa părților solide.“
Notă. In toate formulele de mai jos, dimensiunile măsurate în milimetri, iar densitatea - în grame pe centimetru cub.
Litera reprezintă raportul dintre circumferința raportul său cu diametrul de aproximativ 3.14.
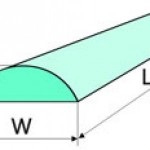
1. Masa tubului (un cilindru gol)
Volumul pereții tubului, unde - diametrul exterior al tubului, - lungimea tubului - grosimea peretelui.
După simplificare obținem formula pentru volumul:
Apoi, masa tubului:
2. Greutate gol (gol) sferă
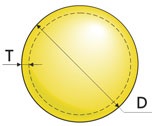
Apoi masa:
3. Greutatea unui segment sferă cav
Deplasarea pereților segmentului minge: unde - diametrul exterior al segmentului de bază, - Segment Elevation - grosimea peretelui *.
După simplificare obținem formula pentru volumul:
Apoi masa:
4. Greutatea unui trunchi de con cav
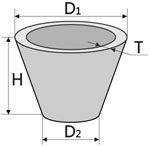
După simplificare obținem formula pentru volumul:
Apoi masa:
5. Greutatea unui trunchi de con cav
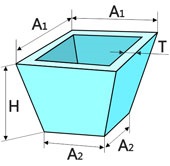
După simplificare obținem formula pentru volumul:
Apoi masa:
* În acest caz - acest lucru nu este destul de grosimea peretelui. Strict vorbind, avem de-a face aici cu două valori: una care stă în formulele ale suportului, tocmai grosimea peretelui, și cel pe care îl ia din afara dimensiunii corpului pentru a obține în interiorul dimensiunea - este grosimea peretelui împărțit cosinusul unghiul de formare. Dar, în cele mai multe cazuri, grosimea peretelui nu depășește un procent mic de marimea corpului, iar eroarea poate fi neglijată. Cu toate acestea, pentru componentele cu pereții groși trebuie să fie luat în considerare această circumstanță.
înregistrări similare